Question Number 8929 by kuldeep singh raj last updated on 06/Nov/16

Commented by Rasheed Soomro last updated on 06/Nov/16

$$\mathrm{This}\:\mathrm{depends}\:\mathrm{upon}\:\mathrm{the}\:\mathrm{position}\:\mathrm{of}\:\mathrm{C}. \\ $$$$\mathrm{For}\:\mathrm{example}\:\mathrm{how}\:\mathrm{far}\:\mathrm{is}\:\mathrm{C}\:\mathrm{from}\:\mathrm{A}. \\ $$$$\mathrm{So}\:\mathrm{additional}\:\:\mathrm{information}\:\mathrm{is}\:\mathrm{required} \\ $$$$\mathrm{to}\:\mathrm{make}\:\theta\:\mathrm{unique}. \\ $$$$\mathrm{However}\:\mathrm{we}\:\mathrm{can}\:\:\mathrm{restrict}\:\theta: \\ $$$$\mathrm{0}<\theta<\mathrm{55} \\ $$
Answered by FilupSmith last updated on 06/Nov/16
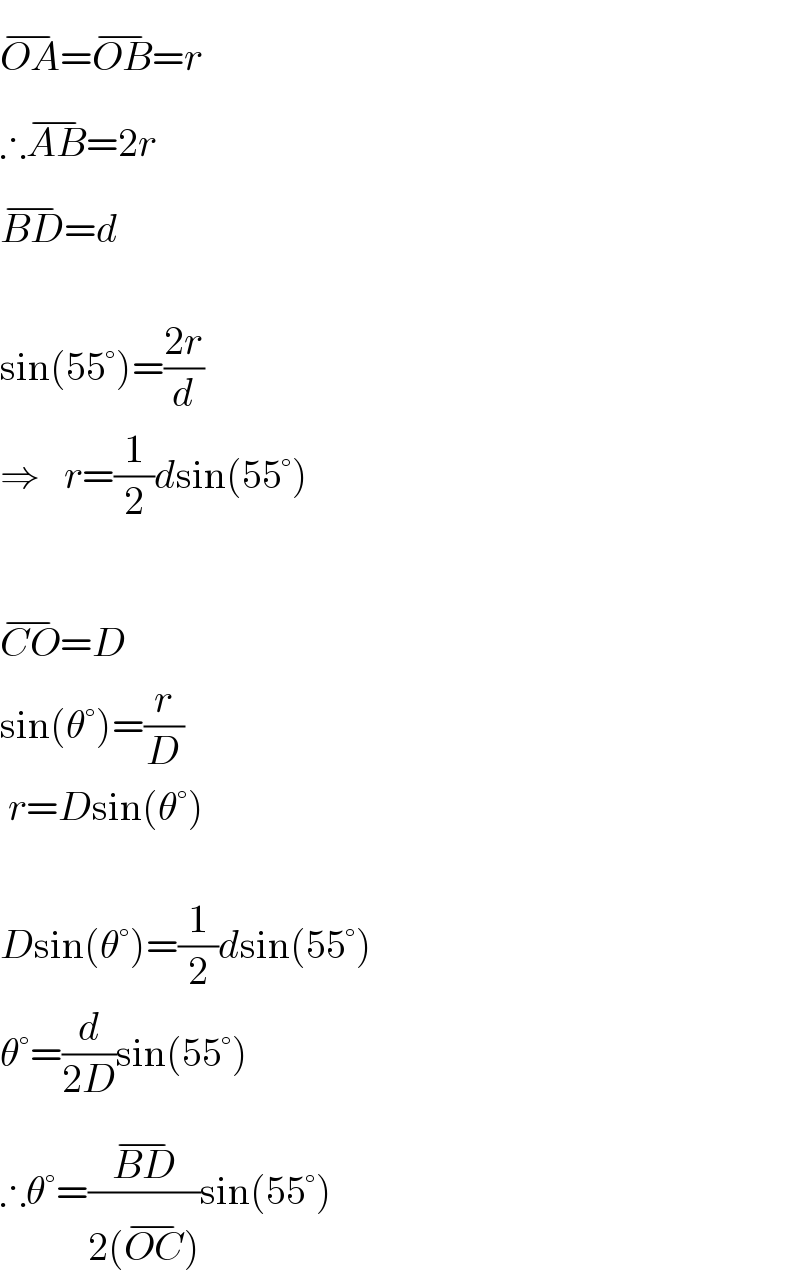
$$\overline {{OA}}=\overline {{OB}}={r} \\ $$$$\therefore\overline {{AB}}=\mathrm{2}{r} \\ $$$$\overline {{BD}}={d} \\ $$$$\: \\ $$$$\mathrm{sin}\left(\mathrm{55}°\right)=\frac{\mathrm{2}{r}}{{d}} \\ $$$$\Rightarrow\:\:\:{r}=\frac{\mathrm{1}}{\mathrm{2}}{d}\mathrm{sin}\left(\mathrm{55}°\right) \\ $$$$\: \\ $$$$\overline {{CO}}={D} \\ $$$$\mathrm{sin}\left(\theta°\right)=\frac{{r}}{{D}} \\ $$$$\:{r}={D}\mathrm{sin}\left(\theta°\right) \\ $$$$\: \\ $$$${D}\mathrm{sin}\left(\theta°\right)=\frac{\mathrm{1}}{\mathrm{2}}{d}\mathrm{sin}\left(\mathrm{55}°\right) \\ $$$$\theta°=\frac{{d}}{\mathrm{2}{D}}\mathrm{sin}\left(\mathrm{55}°\right) \\ $$$$\therefore\theta°=\frac{\overline {{BD}}}{\mathrm{2}\left(\overline {{OC}}\right)}\mathrm{sin}\left(\mathrm{55}°\right) \\ $$
Commented by Rasheed Soomro last updated on 06/Nov/16

$${D}\mathrm{sin}\left(\theta°\right)=\frac{\mathrm{1}}{\mathrm{2}}{d}\mathrm{sin}\left(\mathrm{55}°\right)\overset{???} {\Rightarrow}\theta°=\frac{{d}}{\mathrm{2}{D}}\mathrm{sin}\left(\mathrm{55}°\right) \\ $$$$ \\ $$
Commented by FilupSmith last updated on 06/Nov/16

$$\mathrm{sorry},\:\mathrm{i}\:\mathrm{mean}: \\ $$$$\theta°=\mathrm{arcsin}\left(\frac{{d}}{\mathrm{2}{D}}\mathrm{sin}\left(\mathrm{55}°\right)\right) \\ $$
