Menu Close

solve-the-equation-cos-2001-x-sin-2001-1-

Tinku Tara 0 Comments
Pin




Question Number 722 by malwaan1 last updated on 04/Mar/15
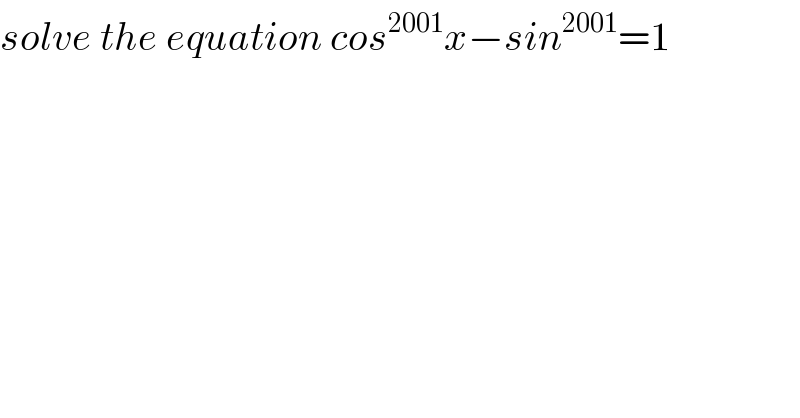
solve the equation cos^(2001) x−sin^(2001) =1
$${solve}\:{the}\:{equation}\:{cos}^{\mathrm{2001}} {x}−{sin}^{\mathrm{2001}} =\mathrm{1} \\ $$$$ \\ $$
Commented by malwaan last updated on 04/Mar/15
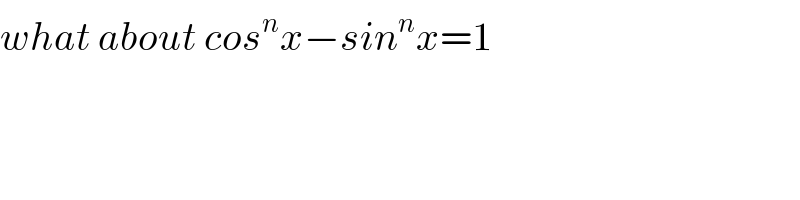
what about cos^n x−sin^n x=1
$${what}\:{about}\:{cos}^{{n}} {x}−{sin}^{{n}} {x}=\mathrm{1}\:\: \\ $$
Commented by prakash jain last updated on 04/Mar/15
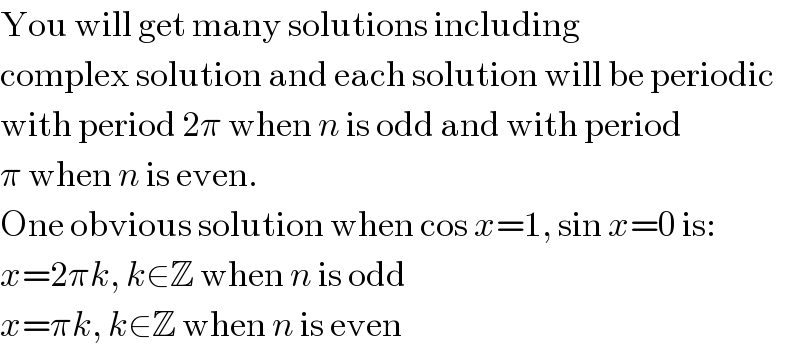
You will get many solutions including complex solution and each solution will be periodic with period 2π when n is odd and with period π when n is even. One obvious solution when cos x=1, sin x=0 is: x=2πk, k∈Z when n is odd x=πk, k∈Z when n is even
$$\mathrm{You}\:\mathrm{will}\:\mathrm{get}\:\mathrm{many}\:\mathrm{solutions}\:\mathrm{including} \\ $$$$\mathrm{complex}\:\mathrm{solution}\:\mathrm{and}\:\mathrm{each}\:\mathrm{solution}\:\mathrm{will}\:\mathrm{be}\:\mathrm{periodic} \\ $$$$\mathrm{with}\:\mathrm{period}\:\mathrm{2}\pi\:\mathrm{when}\:{n}\:\mathrm{is}\:\mathrm{odd}\:\mathrm{and}\:\mathrm{with}\:\mathrm{period} \\ $$$$\pi\:\mathrm{when}\:{n}\:\mathrm{is}\:\mathrm{even}. \\ $$$$\mathrm{One}\:\mathrm{obvious}\:\mathrm{solution}\:\mathrm{when}\:\mathrm{cos}\:{x}=\mathrm{1},\:\mathrm{sin}\:{x}=\mathrm{0}\:\mathrm{is}: \\ $$$${x}=\mathrm{2}\pi{k},\:{k}\in\mathbb{Z}\:\mathrm{when}\:{n}\:\mathrm{is}\:\mathrm{odd} \\ $$$${x}=\pi{k},\:{k}\in\mathbb{Z}\:\mathrm{when}\:{n}\:\mathrm{is}\:\mathrm{even} \\ $$
Answered by prakash jain last updated on 05/Mar/15
y=e^(ix) cos x=((y^2 +1)/(2y)) sin x=((y^2 −1)/(2iy)) cos^n x−sin^n x=1 (((y^2 +1)/(2y)))^n −(((y^2 +1)/(2iy)))^n =1 This given an equation which need to be solved in y. Then you can find x.
$${y}={e}^{{ix}} \\ $$$$\mathrm{cos}\:{x}=\frac{{y}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{y}} \\ $$$$\mathrm{sin}\:{x}=\frac{{y}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{iy}} \\ $$$$\mathrm{cos}^{{n}} {x}−\mathrm{sin}^{{n}} {x}=\mathrm{1} \\ $$$$\left(\frac{{y}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{y}}\right)^{{n}} −\left(\frac{{y}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{iy}}\right)^{{n}} =\mathrm{1} \\ $$$$\mathrm{This}\:\mathrm{given}\:\mathrm{an}\:\mathrm{equation}\:\mathrm{which}\:\mathrm{need}\:\mathrm{to} \\ $$$$\mathrm{be}\:\mathrm{solved}\:\mathrm{in}\:{y}.\:\mathrm{Then}\:\mathrm{you}\:\mathrm{can}\:\mathrm{find}\:{x}. \\ $$
Commented by malwaan last updated on 04/Mar/15
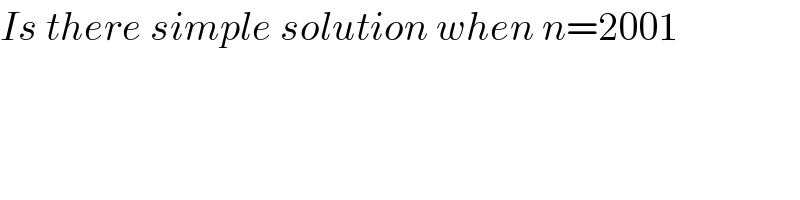
Is there simple solution when n=2001
$${Is}\:{there}\:{simple}\:{solution}\:{when}\:{n}=\mathrm{2001}\: \\ $$
Commented by prakash jain last updated on 04/Mar/15
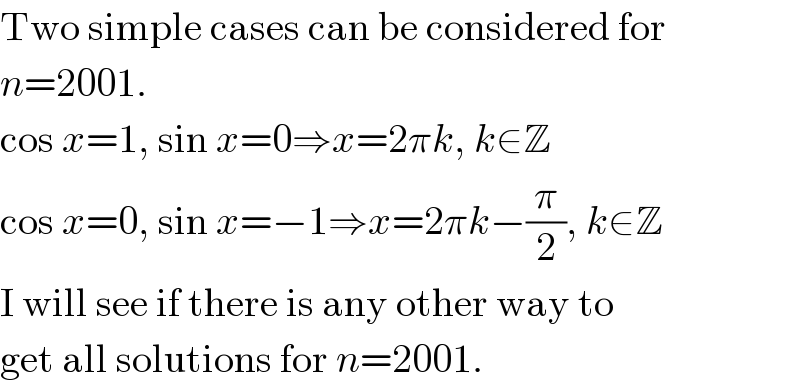
Two simple cases can be considered for n=2001. cos x=1, sin x=0⇒x=2πk, k∈Z cos x=0, sin x=−1⇒x=2πk−(π/2), k∈Z I will see if there is any other way to get all solutions for n=2001.
$$\mathrm{Two}\:\mathrm{simple}\:\mathrm{cases}\:\mathrm{can}\:\mathrm{be}\:\mathrm{considered}\:\mathrm{for} \\ $$$${n}=\mathrm{2001}. \\ $$$$\mathrm{cos}\:{x}=\mathrm{1},\:\mathrm{sin}\:{x}=\mathrm{0}\Rightarrow{x}=\mathrm{2}\pi{k},\:{k}\in\mathbb{Z} \\ $$$$\mathrm{cos}\:{x}=\mathrm{0},\:\mathrm{sin}\:{x}=−\mathrm{1}\Rightarrow{x}=\mathrm{2}\pi{k}−\frac{\pi}{\mathrm{2}},\:{k}\in\mathbb{Z} \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{see}\:\mathrm{if}\:\mathrm{there}\:\mathrm{is}\:\mathrm{any}\:\mathrm{other}\:\mathrm{way}\:\mathrm{to} \\ $$$$\mathrm{get}\:\mathrm{all}\:\mathrm{solutions}\:\mathrm{for}\:{n}=\mathrm{2001}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *