Question Number 74509 by ajfour last updated on 25/Nov/19

Commented by ajfour last updated on 25/Nov/19
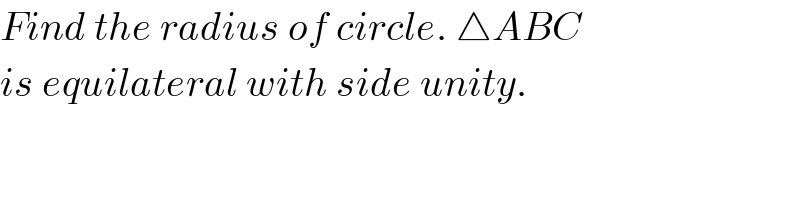
$${Find}\:{the}\:{radius}\:{of}\:{circle}.\:\bigtriangleup{ABC} \\ $$$${is}\:{equilateral}\:{with}\:{side}\:{unity}. \\ $$
Commented by ajfour last updated on 25/Nov/19
Commented by ajfour last updated on 25/Nov/19
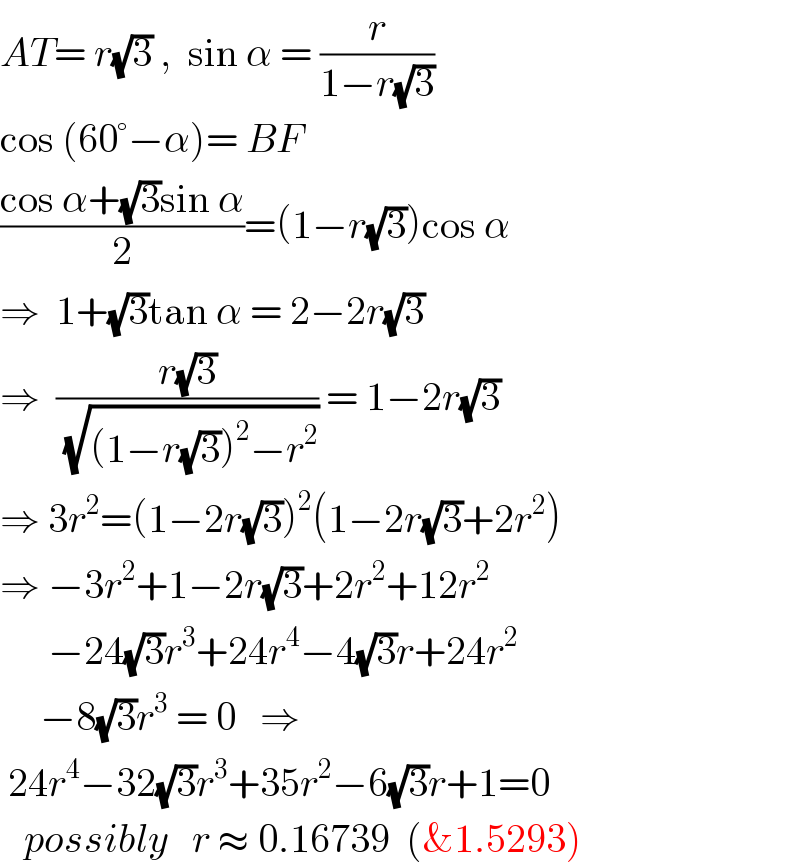
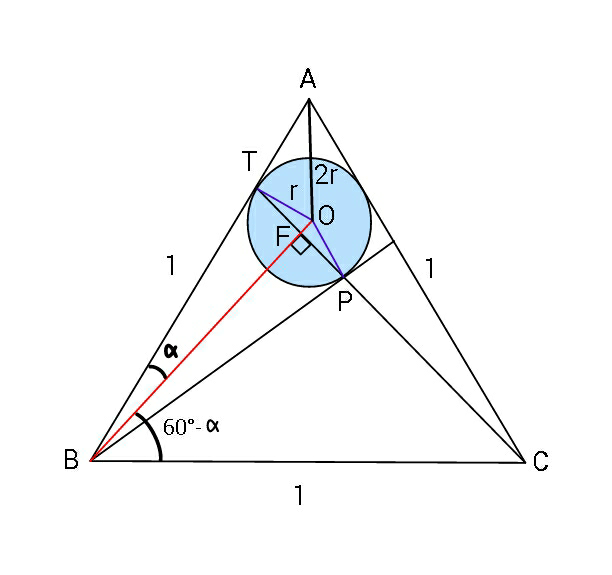
$${AT}=\:{r}\sqrt{\mathrm{3}}\:,\:\:\mathrm{sin}\:\alpha\:=\:\frac{{r}}{\mathrm{1}−{r}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{cos}\:\left(\mathrm{60}°−\alpha\right)=\:{BF} \\ $$$$\frac{\mathrm{cos}\:\alpha+\sqrt{\mathrm{3}}\mathrm{sin}\:\alpha}{\mathrm{2}}=\left(\mathrm{1}−{r}\sqrt{\mathrm{3}}\right)\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\:\:\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{tan}\:\alpha\:=\:\mathrm{2}−\mathrm{2}{r}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\:\frac{{r}\sqrt{\mathrm{3}}}{\:\sqrt{\left(\mathrm{1}−{r}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }}\:=\:\mathrm{1}−\mathrm{2}{r}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{3}{r}^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{2}{r}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{r}\sqrt{\mathrm{3}}+\mathrm{2}{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:−\mathrm{3}{r}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{r}\sqrt{\mathrm{3}}+\mathrm{2}{r}^{\mathrm{2}} +\mathrm{12}{r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:−\mathrm{24}\sqrt{\mathrm{3}}{r}^{\mathrm{3}} +\mathrm{24}{r}^{\mathrm{4}} −\mathrm{4}\sqrt{\mathrm{3}}{r}+\mathrm{24}{r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:−\mathrm{8}\sqrt{\mathrm{3}}{r}^{\mathrm{3}} \:=\:\mathrm{0}\:\:\:\Rightarrow \\ $$$$\:\mathrm{24}{r}^{\mathrm{4}} −\mathrm{32}\sqrt{\mathrm{3}}{r}^{\mathrm{3}} +\mathrm{35}{r}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{3}}{r}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:{possibly}\:\:\:{r}\:\approx\:\mathrm{0}.\mathrm{16739}\:\:\left(\&\mathrm{1}.\mathrm{5293}\right) \\ $$
Commented by ajfour last updated on 25/Nov/19

