Prove-that-for-p-q-r-N-lcm-p-q-r-gcd-p-q-r-p-q-r-gcd-p-q-gcd-q-r-gcd-r-p-

Question Number 66275 by Rasheed.Sindhi last updated on 12/Aug/19

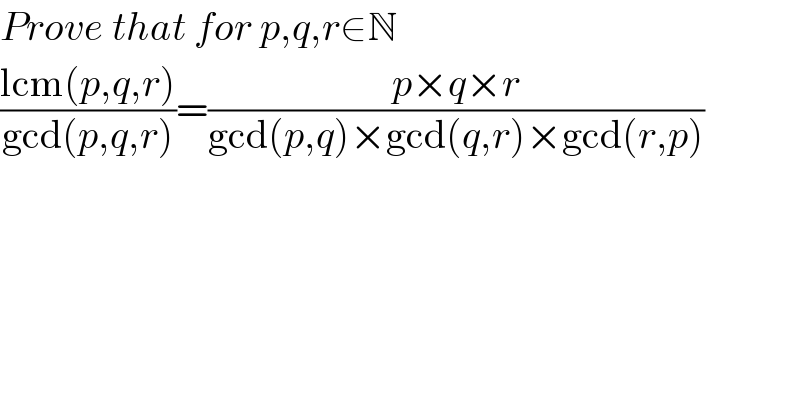
$${Prove}\:{that}\:{for}\:{p},{q},{r}\in\mathbb{N} \\ $$$$\frac{\mathrm{lcm}\left({p},{q},{r}\right)}{\mathrm{gcd}\left({p},{q},{r}\right)}=\frac{{p}×{q}×{r}}{\mathrm{gcd}\left({p},{q}\right)×\mathrm{gcd}\left({q},{r}\right)×\mathrm{gcd}\left({r},{p}\right)} \\ $$

Commented by Prithwish sen last updated on 12/Aug/19

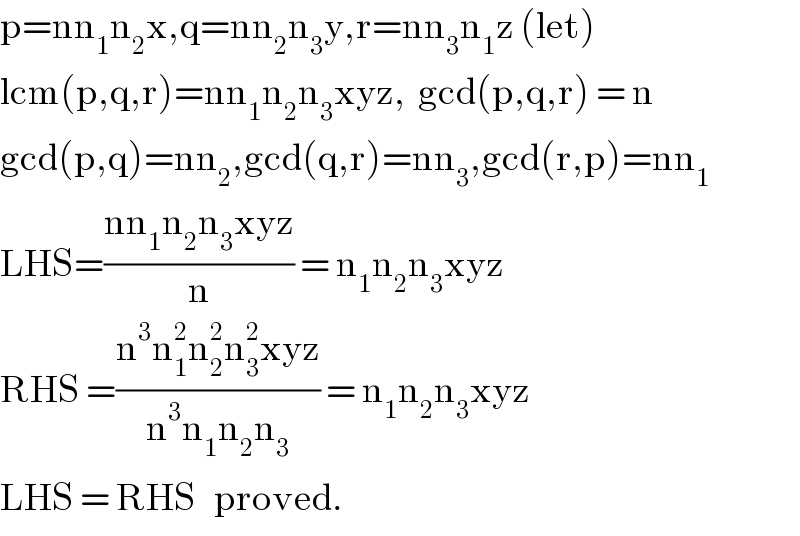
p=nn_1 n_2 x,q=nn_2 n_3 y,r=nn_3 n_1 z (let) lcm(p,q,r)=nn_1 n_2 n_3 xyz, gcd(p,q,r) = n gcd(p,q)=nn_2 ,gcd(q,r)=nn_3 ,gcd(r,p)=nn_1 LHS=((nn_1 n_2 n_3 xyz)/n) = n_1 n_2 n_3 xyz RHS =((n^3 n_1 ^2 n_2 ^2 n_3 ^2 xyz)/(n^3 n_1 n_2 n_3 )) = n_1 n_2 n_3 xyz LHS = RHS proved.

$$\mathrm{p}=\mathrm{nn}_{\mathrm{1}} \mathrm{n}_{\mathrm{2}} \mathrm{x},\mathrm{q}=\mathrm{nn}_{\mathrm{2}} \mathrm{n}_{\mathrm{3}} \mathrm{y},\mathrm{r}=\mathrm{nn}_{\mathrm{3}} \mathrm{n}_{\mathrm{1}} \mathrm{z}\:\left(\mathrm{let}\right) \\ $$$$\mathrm{lcm}\left(\mathrm{p},\mathrm{q},\mathrm{r}\right)=\mathrm{nn}_{\mathrm{1}} \mathrm{n}_{\mathrm{2}} \mathrm{n}_{\mathrm{3}} \mathrm{xyz},\:\:\mathrm{gcd}\left(\mathrm{p},\mathrm{q},\mathrm{r}\right)\:=\:\mathrm{n} \\ $$$$\mathrm{gcd}\left(\mathrm{p},\mathrm{q}\right)=\mathrm{nn}_{\mathrm{2}} ,\mathrm{gcd}\left(\mathrm{q},\mathrm{r}\right)=\mathrm{nn}_{\mathrm{3}} ,\mathrm{gcd}\left(\mathrm{r},\mathrm{p}\right)=\mathrm{nn}_{\mathrm{1}} \\ $$$$\mathrm{LHS}=\frac{\mathrm{nn}_{\mathrm{1}} \mathrm{n}_{\mathrm{2}} \mathrm{n}_{\mathrm{3}} \mathrm{xyz}}{\mathrm{n}}\:=\:\mathrm{n}_{\mathrm{1}} \mathrm{n}_{\mathrm{2}} \mathrm{n}_{\mathrm{3}} \mathrm{xyz} \\ $$$$\mathrm{RHS}\:=\frac{\mathrm{n}^{\mathrm{3}} \mathrm{n}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{n}_{\mathrm{2}} ^{\mathrm{2}} \mathrm{n}_{\mathrm{3}} ^{\mathrm{2}} \mathrm{xyz}}{\mathrm{n}^{\mathrm{3}} \mathrm{n}_{\mathrm{1}} \mathrm{n}_{\mathrm{2}} \mathrm{n}_{\mathrm{3}} }\:=\:\mathrm{n}_{\mathrm{1}} \mathrm{n}_{\mathrm{2}} \mathrm{n}_{\mathrm{3}} \mathrm{xyz} \\ $$$$\mathrm{LHS}\:=\:\mathrm{RHS}\:\:\:\mathrm{proved}. \\ $$

Commented by Rasheed.Sindhi last updated on 13/Aug/19

$$\mathcal{T}{hanks}\:{Sir}! \\ $$

Facebook Tweet Pin

Prove-that-for-p-q-r-N-lcm-p-q-r-gcd-p-q-r-p-q-r-gcd-p-q-gcd-q-r-gcd-r-p-

Leave a Reply Cancel reply