Menu Close

Value-of-maximum-f-x-2-log-x-5-2-log-3-x-is-a-4-b-8-c-12-d-15-e-16-

Tinku Tara 0 Comments
Pin




Question Number 66279 by gunawan last updated on 12/Aug/19
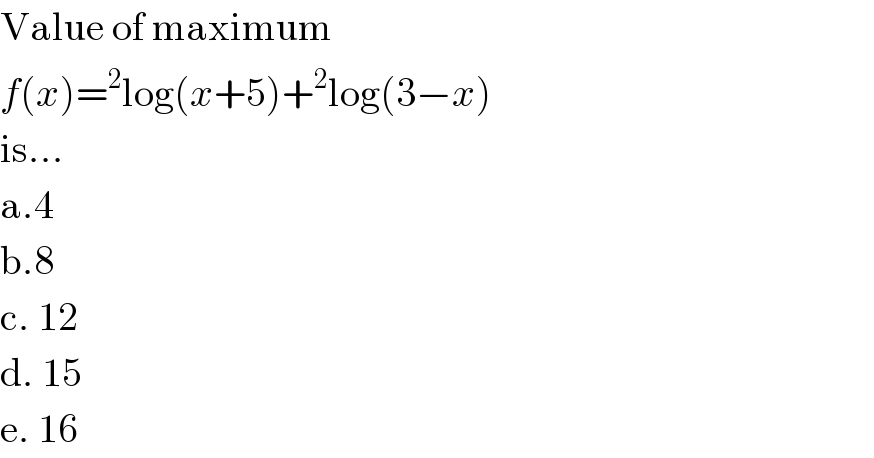
Value of maximum f(x)=^2 log(x+5)+^2 log(3−x) is... a.4 b.8 c. 12 d. 15 e. 16
$$\mathrm{Value}\:\mathrm{of}\:\mathrm{maximum} \\ $$$${f}\left({x}\right)=^{\mathrm{2}} \mathrm{log}\left({x}+\mathrm{5}\right)+^{\mathrm{2}} \mathrm{log}\left(\mathrm{3}−{x}\right) \\ $$$$\mathrm{is}… \\ $$$$\mathrm{a}.\mathrm{4} \\ $$$$\mathrm{b}.\mathrm{8} \\ $$$$\mathrm{c}.\:\mathrm{12} \\ $$$$\mathrm{d}.\:\mathrm{15} \\ $$$$\mathrm{e}.\:\mathrm{16} \\ $$
Commented by mathmax by abdo last updated on 12/Aug/19
f(x)=log_2 (x+5)+log_2 (3−x) x∈D_f ⇔x+5>0 and 3−x>0 ⇔−5<x<3 ⇒D_f =]−5,3[ f(x) =(1/(ln(2))){ln(x+5)+ln(3−x)} ⇒f^′ (x)=(1/(ln2)){(1/(x+5))−(1/(3−x))} =(1/(ln2)){((3−x−x−5)/((x+5)(3−x)))} =(1/(ln(2))){((−2−2x)/((x+5)(3−x)))} =((−2)/(ln2)){((x+1)/((x+5)(3−x)))} so f^′ (x)=0 ⇔x=−1 variation of f(x) x −5 −1 3 f^′ (x) + 0 − f(x) −∞ inc f(−1)decr −∞ max f(x)= f(−1)=(1/(ln(2))){2ln(2)+2ln(2)} =4 x∈D_f the correct answer is a)
$${f}\left({x}\right)={log}_{\mathrm{2}} \left({x}+\mathrm{5}\right)+{log}_{\mathrm{2}} \left(\mathrm{3}−{x}\right)\:\:\: \\ $$$$\left.{x}\in{D}_{{f}} \Leftrightarrow{x}+\mathrm{5}>\mathrm{0}\:{and}\:\mathrm{3}−{x}>\mathrm{0}\:\Leftrightarrow−\mathrm{5}<{x}<\mathrm{3}\:\Rightarrow{D}_{{f}} =\right]−\mathrm{5},\mathrm{3}\left[\right. \\ $$$${f}\left({x}\right)\:=\frac{\mathrm{1}}{{ln}\left(\mathrm{2}\right)}\left\{{ln}\left({x}+\mathrm{5}\right)+{ln}\left(\mathrm{3}−{x}\right)\right\}\:\Rightarrow{f}^{'} \left({x}\right)=\frac{\mathrm{1}}{{ln}\mathrm{2}}\left\{\frac{\mathrm{1}}{{x}+\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{3}−{x}}\right\} \\ $$$$=\frac{\mathrm{1}}{{ln}\mathrm{2}}\left\{\frac{\mathrm{3}−{x}−{x}−\mathrm{5}}{\left({x}+\mathrm{5}\right)\left(\mathrm{3}−{x}\right)}\right\}\:=\frac{\mathrm{1}}{{ln}\left(\mathrm{2}\right)}\left\{\frac{−\mathrm{2}−\mathrm{2}{x}}{\left({x}+\mathrm{5}\right)\left(\mathrm{3}−{x}\right)}\right\} \\ $$$$=\frac{−\mathrm{2}}{{ln}\mathrm{2}}\left\{\frac{{x}+\mathrm{1}}{\left({x}+\mathrm{5}\right)\left(\mathrm{3}−{x}\right)}\right\}\:{so}\:{f}^{'} \left({x}\right)=\mathrm{0}\:\Leftrightarrow{x}=−\mathrm{1} \\ $$$${variation}\:{of}\:{f}\left({x}\right)\: \\ $$$${x}\:\:\:\:\:\:\:\:\:−\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3} \\ $$$${f}^{'} \left({x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:− \\ $$$${f}\left({x}\right)\:\:\:−\infty\:\:\:\:\:{inc}\:\:\:\:\:{f}\left(−\mathrm{1}\right){decr}\:\:\:\:\:\:\:\:−\infty \\ $$$${max}\:{f}\left({x}\right)=\:\:{f}\left(−\mathrm{1}\right)=\frac{\mathrm{1}}{{ln}\left(\mathrm{2}\right)}\left\{\mathrm{2}{ln}\left(\mathrm{2}\right)+\mathrm{2}{ln}\left(\mathrm{2}\right)\right\}\:=\mathrm{4} \\ $$$${x}\in{D}_{{f}} \\ $$$$\left.{the}\:{correct}\:{answer}\:{is}\:{a}\right) \\ $$
Answered by Kunal12588 last updated on 12/Aug/19
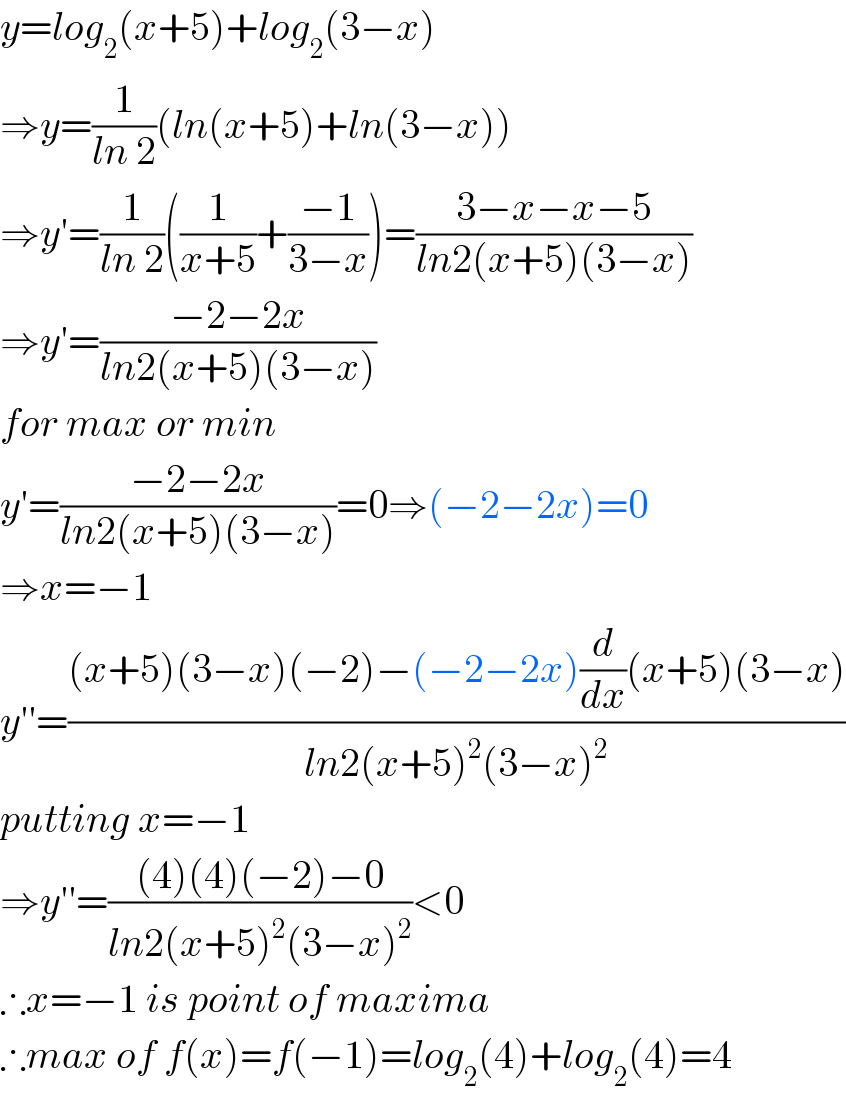
y=log_2 (x+5)+log_2 (3−x) ⇒y=(1/(ln 2))(ln(x+5)+ln(3−x)) ⇒y′=(1/(ln 2))((1/(x+5))+((−1)/(3−x)))=((3−x−x−5)/(ln2(x+5)(3−x))) ⇒y′=((−2−2x)/(ln2(x+5)(3−x))) for max or min y′=((−2−2x)/(ln2(x+5)(3−x)))=0⇒(−2−2x)=0 ⇒x=−1 y′′=(((x+5)(3−x)(−2)−(−2−2x)(d/dx)(x+5)(3−x))/(ln2(x+5)^2 (3−x)^2 )) putting x=−1 ⇒y′′=(((4)(4)(−2)−0)/(ln2(x+5)^2 (3−x)^2 ))<0 ∴x=−1 is point of maxima ∴max of f(x)=f(−1)=log_2 (4)+log_2 (4)=4
$${y}={log}_{\mathrm{2}} \left({x}+\mathrm{5}\right)+{log}_{\mathrm{2}} \left(\mathrm{3}−{x}\right) \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{{ln}\:\mathrm{2}}\left({ln}\left({x}+\mathrm{5}\right)+{ln}\left(\mathrm{3}−{x}\right)\right) \\ $$$$\Rightarrow{y}'=\frac{\mathrm{1}}{{ln}\:\mathrm{2}}\left(\frac{\mathrm{1}}{{x}+\mathrm{5}}+\frac{−\mathrm{1}}{\mathrm{3}−{x}}\right)=\frac{\mathrm{3}−{x}−{x}−\mathrm{5}}{{ln}\mathrm{2}\left({x}+\mathrm{5}\right)\left(\mathrm{3}−{x}\right)} \\ $$$$\Rightarrow{y}'=\frac{−\mathrm{2}−\mathrm{2}{x}}{{ln}\mathrm{2}\left({x}+\mathrm{5}\right)\left(\mathrm{3}−{x}\right)} \\ $$$${for}\:{max}\:{or}\:{min} \\ $$$${y}'=\frac{−\mathrm{2}−\mathrm{2}{x}}{{ln}\mathrm{2}\left({x}+\mathrm{5}\right)\left(\mathrm{3}−{x}\right)}=\mathrm{0}\Rightarrow\left(−\mathrm{2}−\mathrm{2}{x}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{1} \\ $$$${y}''=\frac{\left({x}+\mathrm{5}\right)\left(\mathrm{3}−{x}\right)\left(−\mathrm{2}\right)−\left(−\mathrm{2}−\mathrm{2}{x}\right)\frac{{d}}{{dx}}\left({x}+\mathrm{5}\right)\left(\mathrm{3}−{x}\right)}{{ln}\mathrm{2}\left({x}+\mathrm{5}\right)^{\mathrm{2}} \left(\mathrm{3}−{x}\right)^{\mathrm{2}} } \\ $$$${putting}\:{x}=−\mathrm{1} \\ $$$$\Rightarrow{y}''=\frac{\left(\mathrm{4}\right)\left(\mathrm{4}\right)\left(−\mathrm{2}\right)−\mathrm{0}}{{ln}\mathrm{2}\left({x}+\mathrm{5}\right)^{\mathrm{2}} \left(\mathrm{3}−{x}\right)^{\mathrm{2}} }<\mathrm{0} \\ $$$$\therefore{x}=−\mathrm{1}\:{is}\:{point}\:{of}\:{maxima} \\ $$$$\therefore{max}\:{of}\:{f}\left({x}\right)={f}\left(−\mathrm{1}\right)={log}_{\mathrm{2}} \left(\mathrm{4}\right)+{log}_{\mathrm{2}} \left(\mathrm{4}\right)=\mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *