Question Number 140205 by EnterUsername last updated on 05/May/21

$${ABCD}\:\mathrm{is}\:\mathrm{a}\:\mathrm{rhombus}.\:\mathrm{Its}\:\mathrm{diagonals}\:{AC}\:\mathrm{and}\:{BD}\:\mathrm{inter}- \\ $$$$\mathrm{sect}\:\mathrm{at}\:{M}\:\mathrm{and}\:\mathrm{satisfy}\:{BD}=\mathrm{2}{AC}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{points}\:{D}\:\mathrm{and} \\ $$$${M}\:\mathrm{are}\:\mathrm{represented}\:\mathrm{by}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{numbers}\:\mathrm{1}+{i}\:\mathrm{and} \\ $$$$\mathrm{2}−{i},\:\mathrm{respectively},\:\mathrm{then}\:{A}\:\mathrm{is}\:\mathrm{represented}\:\mathrm{by} \\ $$$$\left(\mathrm{A}\right)\:\mathrm{3}−{i}/\mathrm{2}\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\mathrm{3}+{i}/\mathrm{2}\:\:\:\:\:\:\:\:\:\left(\mathrm{C}\right)\:\mathrm{1}+\mathrm{3}{i}/\mathrm{2}\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\mathrm{1}−\mathrm{3}{i}/\mathrm{2} \\ $$
Answered by mr W last updated on 05/May/21

Commented by EnterUsername last updated on 05/May/21

$$\mathrm{Thank}\:\mathrm{you},\:\mathrm{Sir} \\ $$
Commented by EnterUsername last updated on 05/May/21
Sir, where is the solution ? ��
Commented by mr W last updated on 05/May/21
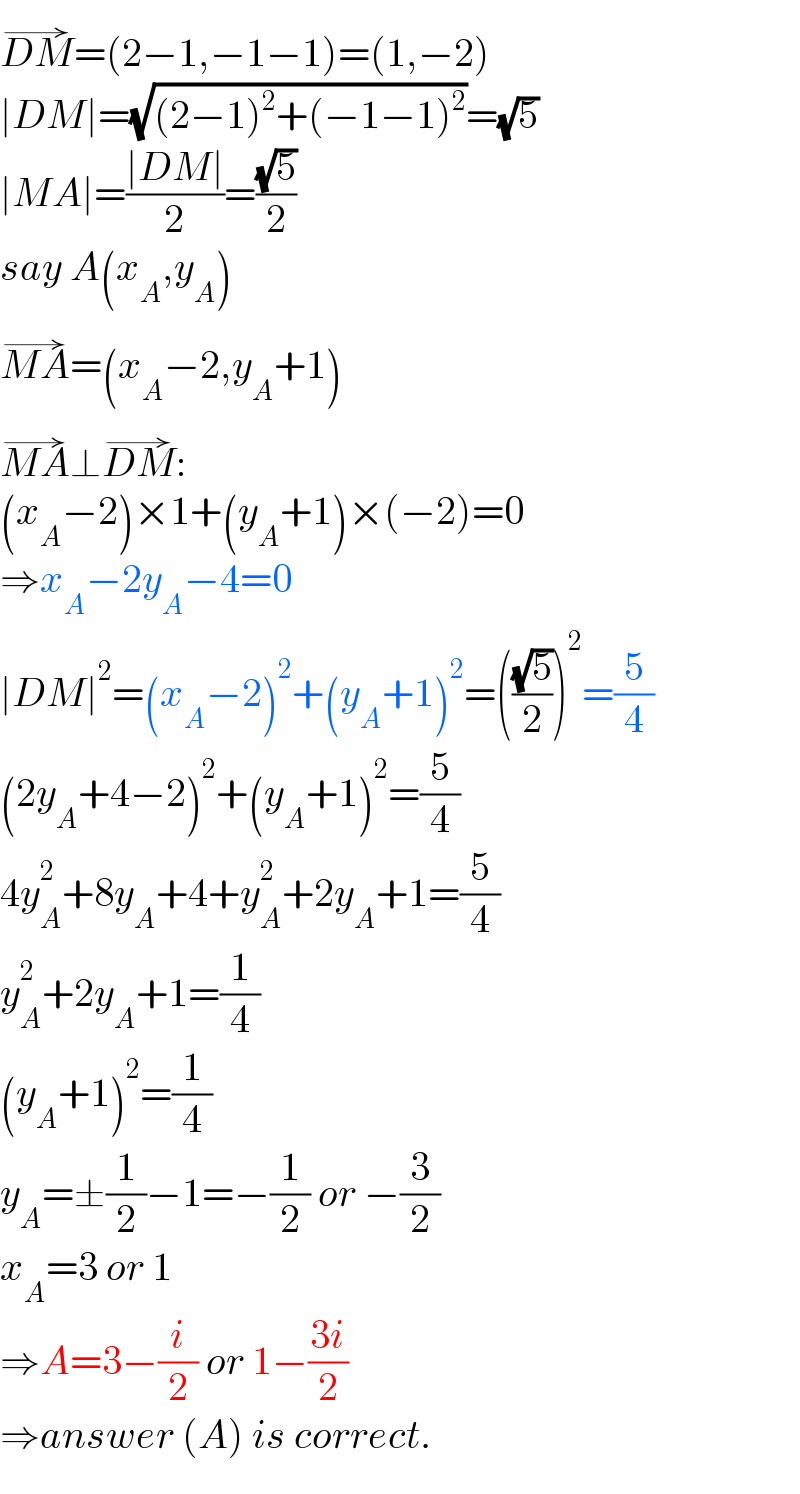
$$\overset{\rightarrow} {{DM}}=\left(\mathrm{2}−\mathrm{1},−\mathrm{1}−\mathrm{1}\right)=\left(\mathrm{1},−\mathrm{2}\right) \\ $$$$\mid{DM}\mid=\sqrt{\left(\mathrm{2}−\mathrm{1}\right)^{\mathrm{2}} +\left(−\mathrm{1}−\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\mathrm{5}} \\ $$$$\mid{MA}\mid=\frac{\mid{DM}\mid}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${say}\:{A}\left({x}_{{A}} ,{y}_{{A}} \right) \\ $$$$\overset{\rightarrow} {{MA}}=\left({x}_{{A}} −\mathrm{2},{y}_{{A}} +\mathrm{1}\right) \\ $$$$\overset{\rightarrow} {{MA}}\bot\overset{\rightarrow} {{DM}}: \\ $$$$\left({x}_{{A}} −\mathrm{2}\right)×\mathrm{1}+\left({y}_{{A}} +\mathrm{1}\right)×\left(−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}_{{A}} −\mathrm{2}{y}_{{A}} −\mathrm{4}=\mathrm{0} \\ $$$$\mid{DM}\mid^{\mathrm{2}} =\left({x}_{{A}} −\mathrm{2}\right)^{\mathrm{2}} +\left({y}_{{A}} +\mathrm{1}\right)^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\left(\mathrm{2}{y}_{{A}} +\mathrm{4}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}_{{A}} +\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{4}{y}_{{A}} ^{\mathrm{2}} +\mathrm{8}{y}_{{A}} +\mathrm{4}+{y}_{{A}} ^{\mathrm{2}} +\mathrm{2}{y}_{{A}} +\mathrm{1}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${y}_{{A}} ^{\mathrm{2}} +\mathrm{2}{y}_{{A}} +\mathrm{1}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left({y}_{{A}} +\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${y}_{{A}} =\pm\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}=−\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${x}_{{A}} =\mathrm{3}\:{or}\:\mathrm{1} \\ $$$$\Rightarrow{A}=\mathrm{3}−\frac{{i}}{\mathrm{2}}\:{or}\:\mathrm{1}−\frac{\mathrm{3}{i}}{\mathrm{2}} \\ $$$$\Rightarrow{answer}\:\left({A}\right)\:{is}\:{correct}. \\ $$
