Question Number 749 by 123456 last updated on 06/Mar/15
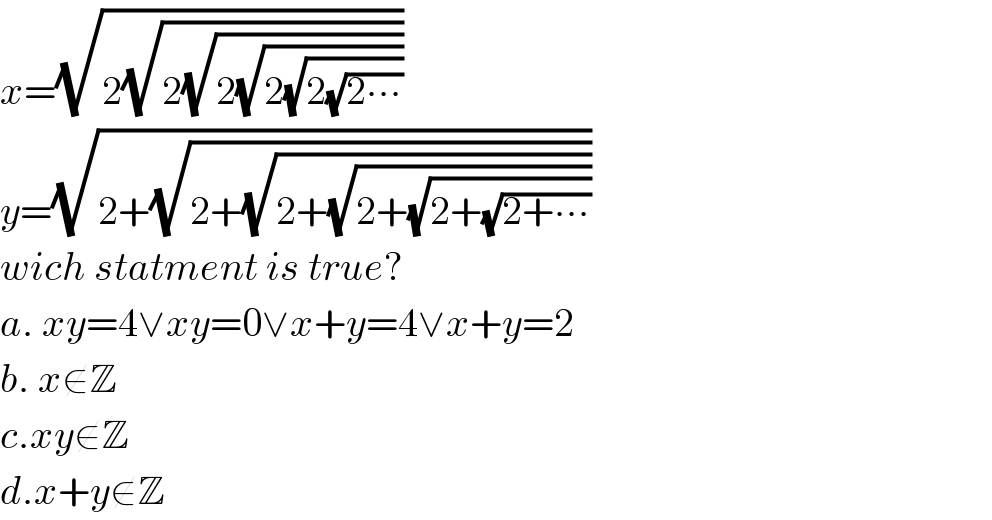
$${x}=\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\centerdot\centerdot\centerdot}}}}}} \\ $$$${y}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\centerdot\centerdot\centerdot}}}}}} \\ $$$${wich}\:{statment}\:{is}\:{true}? \\ $$$${a}.\:{xy}=\mathrm{4}\vee{xy}=\mathrm{0}\vee{x}+{y}=\mathrm{4}\vee{x}+{y}=\mathrm{2} \\ $$$${b}.\:{x}\notin\mathbb{Z} \\ $$$${c}.{xy}\notin\mathbb{Z} \\ $$$${d}.{x}+{y}\notin\mathbb{Z} \\ $$
Answered by prakash jain last updated on 06/Mar/15

$${x}=\sqrt{\mathrm{2}{x}}\Rightarrow{x}^{\mathrm{2}} =\mathrm{2}{x}\Rightarrow{x}=\mathrm{2}\:\because{x}>\mathrm{0} \\ $$$${y}=\sqrt{\mathrm{2}+{y}}\Rightarrow{y}^{\mathrm{2}} =\mathrm{2}+{y}\Rightarrow\left({y}−\mathrm{2}\right)\left({y}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{y}=\mathrm{2}\:\because{y}>\mathrm{0} \\ $$$${a}.\:\boldsymbol{\mathrm{true}}\:{xy}=\mathrm{4},\:{xy}=\mathrm{4} \\ $$$${b}.\:\mathrm{false}\:{x}\in\mathbb{Z} \\ $$$$\mathrm{c}.\:\mathrm{false}\:{xy}\in\mathbb{Z} \\ $$$$\mathrm{d}.\:\mathrm{false}\:{x}+{y}\in\mathbb{Z} \\ $$
