Question Number 74782 by naka3546 last updated on 30/Nov/19
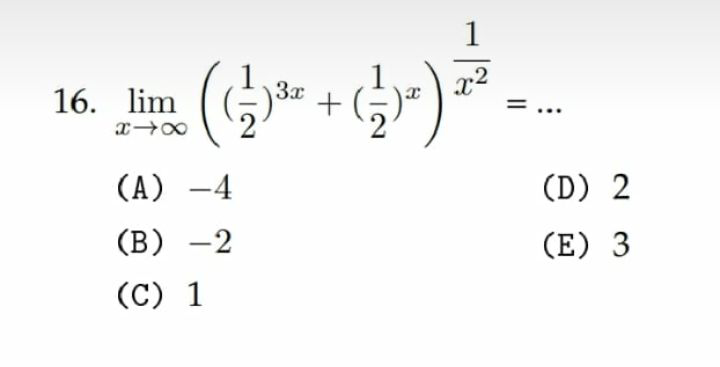
Commented by abdomathmax last updated on 01/Dec/19
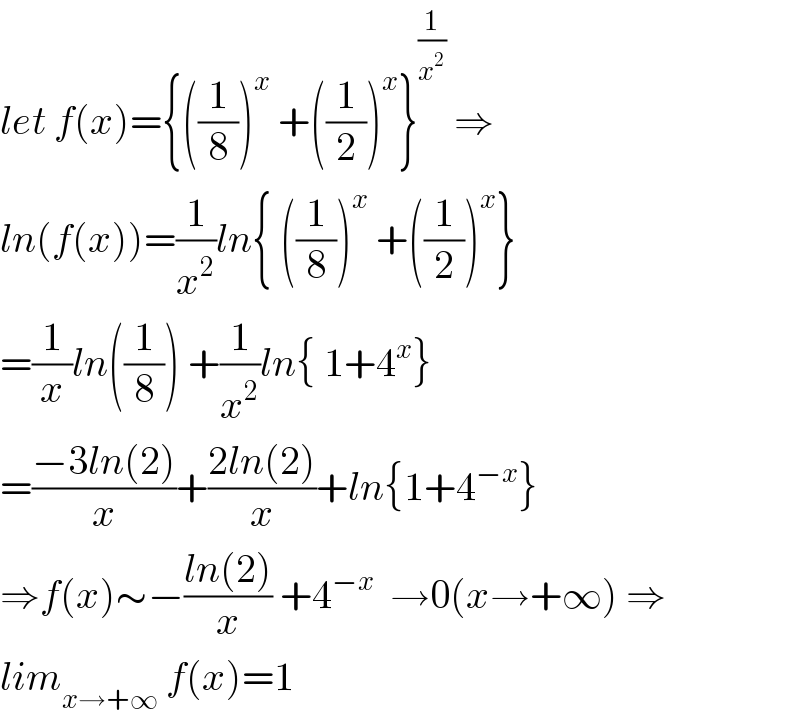
$${let}\:{f}\left({x}\right)=\left\{\left(\frac{\mathrm{1}}{\mathrm{8}}\right)^{{x}} \:+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \right\}^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:\Rightarrow \\ $$$${ln}\left({f}\left({x}\right)\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left\{\:\left(\frac{\mathrm{1}}{\mathrm{8}}\right)^{{x}} \:+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \right\} \\ $$$$=\frac{\mathrm{1}}{{x}}{ln}\left(\frac{\mathrm{1}}{\mathrm{8}}\right)\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left\{\:\mathrm{1}+\mathrm{4}^{{x}} \right\} \\ $$$$=\frac{−\mathrm{3}{ln}\left(\mathrm{2}\right)}{{x}}+\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)}{{x}}+{ln}\left\{\mathrm{1}+\mathrm{4}^{−{x}} \right\} \\ $$$$\Rightarrow{f}\left({x}\right)\sim−\frac{{ln}\left(\mathrm{2}\right)}{{x}}\:+\mathrm{4}^{−{x}} \:\:\rightarrow\mathrm{0}\left({x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} \:{f}\left({x}\right)=\mathrm{1} \\ $$
Commented by abdomathmax last updated on 24/Dec/19
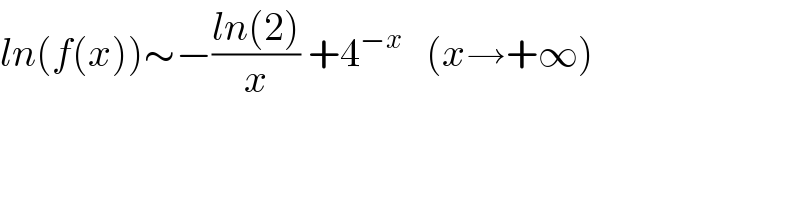
$${ln}\left({f}\left({x}\right)\right)\sim−\frac{{ln}\left(\mathrm{2}\right)}{{x}}\:+\mathrm{4}^{−{x}} \:\:\:\left({x}\rightarrow+\infty\right) \\ $$
Answered by MJS last updated on 30/Nov/19
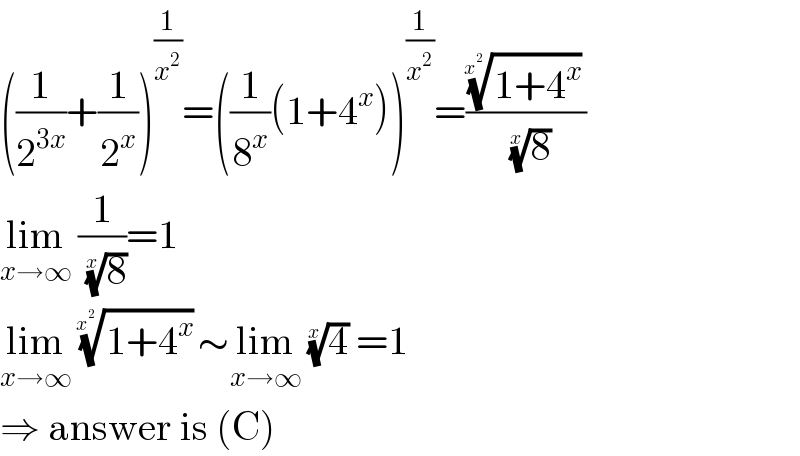
$$\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}{x}} }+\frac{\mathrm{1}}{\mathrm{2}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} =\left(\frac{\mathrm{1}}{\mathrm{8}^{{x}} }\left(\mathrm{1}+\mathrm{4}^{{x}} \right)\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} =\frac{\sqrt[{{x}^{\mathrm{2}} }]{\mathrm{1}+\mathrm{4}^{{x}} }}{\:\sqrt[{{x}}]{\mathrm{8}}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt[{{x}}]{\mathrm{8}}}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{{x}^{\mathrm{2}} }]{\mathrm{1}+\mathrm{4}^{{x}} }\sim\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{{x}}]{\mathrm{4}}\:=\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\left(\mathrm{C}\right) \\ $$
