Question Number 74786 by chess1 last updated on 30/Nov/19

Commented by abdomathmax last updated on 30/Nov/19

$${S}\:=\sum_{{k}=\mathrm{1}} ^{\mathrm{2019}} \:{k}\left(\frac{\mathrm{1}}{\mathrm{2020}}\right)^{{k}} \:={w}\left(\frac{\mathrm{1}}{\mathrm{2020}}\right)\:{with} \\ $$$${w}\left({x}\right)=\sum_{{k}=\mathrm{1}} ^{\mathrm{2019}} \:{kx}^{{k}} \:\:\:{we}\:{have}\:{for}\:{x}\neq\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{0}} ^{\mathrm{2019}} \:{x}^{{k}} \:=\frac{{x}^{\mathrm{2020}} −\mathrm{1}}{{x}−\mathrm{1}}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{\mathrm{2019}} \:{kx}^{{k}−\mathrm{1}} \:=\frac{{d}}{{dx}}\left(\frac{{x}^{\mathrm{2020}} −\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{2020}\:{x}^{\mathrm{2019}} \left({x}−\mathrm{1}\right)−\left({x}^{\mathrm{2020}} −\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2019}\:{x}^{\mathrm{2020}} −\mathrm{2020}\:{x}^{\mathrm{2019}} \:+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{\mathrm{2019}} \:{kx}^{{k}} \:\:=\frac{\mathrm{2019}\:{x}^{\mathrm{2021}} −\mathrm{2020}\:{x}^{\mathrm{2020}} +{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${S}\:=\frac{\mathrm{2019}\left(\frac{\mathrm{1}}{\mathrm{2020}}\right)^{\mathrm{2021}} −\mathrm{2020}\left(\frac{\mathrm{1}}{\mathrm{2020}}\right)^{\mathrm{2020}} +\frac{\mathrm{1}}{\mathrm{2020}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2020}}\right)^{\mathrm{2}} } \\ $$$$ \\ $$
Answered by $@ty@m123 last updated on 01/Dec/19
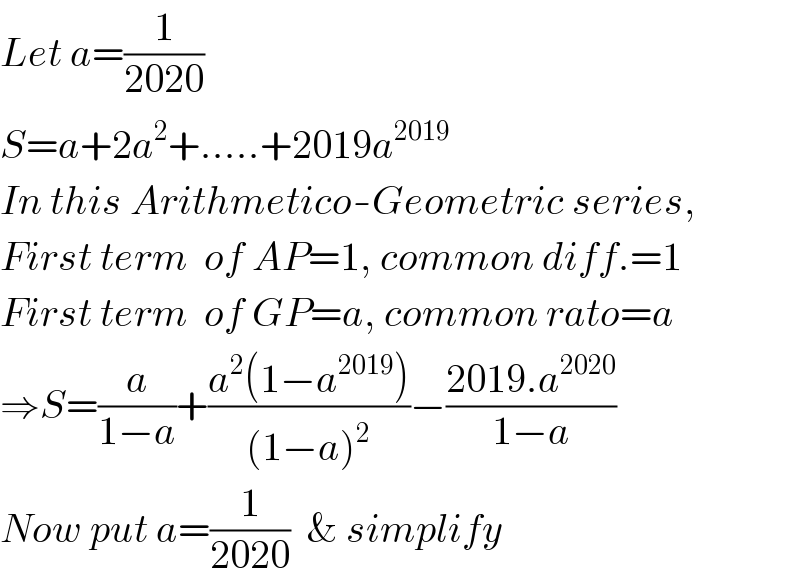
$${Let}\:{a}=\frac{\mathrm{1}}{\mathrm{2020}} \\ $$$${S}={a}+\mathrm{2}{a}^{\mathrm{2}} +…..+\mathrm{2019}{a}^{\mathrm{2019}} \\ $$$${In}\:{this}\:{Arithmetico}-{Geometric}\:{series}, \\ $$$${First}\:{term}\:\:{of}\:{AP}=\mathrm{1},\:{common}\:{diff}.=\mathrm{1} \\ $$$${First}\:{term}\:\:{of}\:{GP}={a},\:{common}\:{rato}={a} \\ $$$$\Rightarrow{S}=\frac{{a}}{\mathrm{1}−{a}}+\frac{{a}^{\mathrm{2}} \left(\mathrm{1}−{a}^{\mathrm{2019}} \right)}{\left(\mathrm{1}−{a}\right)^{\mathrm{2}} }−\frac{\mathrm{2019}.{a}^{\mathrm{2020}} }{\mathrm{1}−{a}} \\ $$$${Now}\:{put}\:{a}=\frac{\mathrm{1}}{\mathrm{2020}}\:\:\&\:{simplify} \\ $$
Answered by mr W last updated on 01/Dec/19

$$\mathrm{1}+{x}+{x}^{\mathrm{2}} +…+{x}^{{n}} =\frac{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{\mathrm{1}−{x}} \\ $$$$\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} …+{nx}^{{n}−\mathrm{1}} =\frac{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }−\frac{\left({n}+\mathrm{1}\right){x}^{{n}} }{\mathrm{1}−{x}} \\ $$$${x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} …+{nx}^{{n}} =\frac{{x}\left(\mathrm{1}−{x}^{{n}+\mathrm{1}} \right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }−\frac{\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} }{\mathrm{1}−{x}} \\ $$$${put}\:{x}=\frac{\mathrm{1}}{\mathrm{2020}},\:{n}=\mathrm{2019}\:{we}\:{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{2020}}+\frac{\mathrm{2}}{\mathrm{2020}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2020}^{\mathrm{3}} }+…+\frac{\mathrm{2019}}{\mathrm{2020}^{\mathrm{2019}} }=\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2020}^{\mathrm{2020}} }}{\mathrm{2020}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2020}}\right)^{\mathrm{2}} }−\frac{\mathrm{2020}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2020}}\right)\mathrm{2020}^{\mathrm{2020}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2020}}+\frac{\mathrm{2}}{\mathrm{2020}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2020}^{\mathrm{3}} }+…+\frac{\mathrm{2019}}{\mathrm{2020}^{\mathrm{2019}} }=\frac{\mathrm{2020}^{\mathrm{2020}} −\mathrm{1}}{\mathrm{2019}^{\mathrm{2}} ×\mathrm{2020}^{\mathrm{2019}} }−\frac{\mathrm{1}}{\mathrm{2019}×\mathrm{2020}^{\mathrm{2018}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2020}}+\frac{\mathrm{2}}{\mathrm{2020}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2020}^{\mathrm{3}} }+…+\frac{\mathrm{2019}}{\mathrm{2020}^{\mathrm{2019}} }=\frac{\mathrm{2020}\left(\mathrm{2020}^{\mathrm{2019}} −\mathrm{2019}\right)−\mathrm{1}}{\mathrm{2019}^{\mathrm{2}} ×\mathrm{2020}^{\mathrm{2019}} } \\ $$
Commented by chess1 last updated on 01/Dec/19

$$\mathrm{thanks} \\ $$
