Question Number 74793 by mathmax by abdo last updated on 30/Nov/19
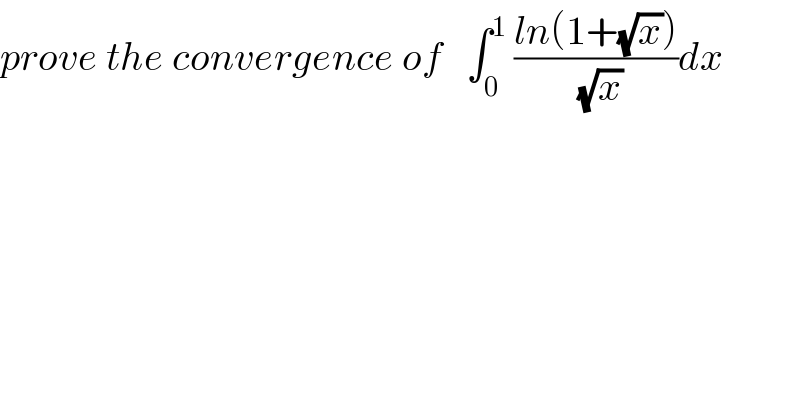
$${prove}\:{the}\:{convergence}\:{of}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+\sqrt{{x}}\right)}{\:\sqrt{{x}}}{dx} \\ $$
Commented by mathmax by abdo last updated on 06/Dec/19
![I=∫_0 ^1 ((ln(1+(√x)))/( (√x)))dx changement (√x)=t give x=t^2 ⇒ I =∫_0 ^1 ((ln(1+t))/t)(2t)dt =2 ∫_0 ^1 ln(1+t)dt =_(1+t=u) 2∫_1 ^2 ln(u)du =2[ulnu−u]_1 ^2 =2{2ln(2)−2+1} =4ln(2)−2](https://www.tinkutara.com/question/Q75057.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+\sqrt{{x}}\right)}{\:\sqrt{{x}}}{dx}\:\:{changement}\:\sqrt{{x}}={t}\:{give}\:{x}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}\left(\mathrm{2}{t}\right){dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}\right){dt}\:=_{\mathrm{1}+{t}={u}} \:\:\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{2}} {ln}\left({u}\right){du} \\ $$$$=\mathrm{2}\left[{ulnu}−{u}\right]_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{2}\left\{\mathrm{2}{ln}\left(\mathrm{2}\right)−\mathrm{2}+\mathrm{1}\right\}\:=\mathrm{4}{ln}\left(\mathrm{2}\right)−\mathrm{2} \\ $$
Answered by mind is power last updated on 01/Dec/19
![u=(√x)⇒du=(1/(2(√x)))dx ∫_0 ^1 2ln(1+u)du=[2(u+1)ln(u+1)−2u]_0 ^1 =4ln(2)−2](https://www.tinkutara.com/question/Q74815.png)
$$\mathrm{u}=\sqrt{\mathrm{x}}\Rightarrow\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2ln}\left(\mathrm{1}+\mathrm{u}\right)\mathrm{du}=\left[\mathrm{2}\left(\mathrm{u}+\mathrm{1}\right)\mathrm{ln}\left(\mathrm{u}+\mathrm{1}\right)−\mathrm{2u}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{4ln}\left(\mathrm{2}\right)−\mathrm{2} \\ $$
