Menu Close

find-x-3-x-1-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 74890 by abdomathmax last updated on 03/Dec/19
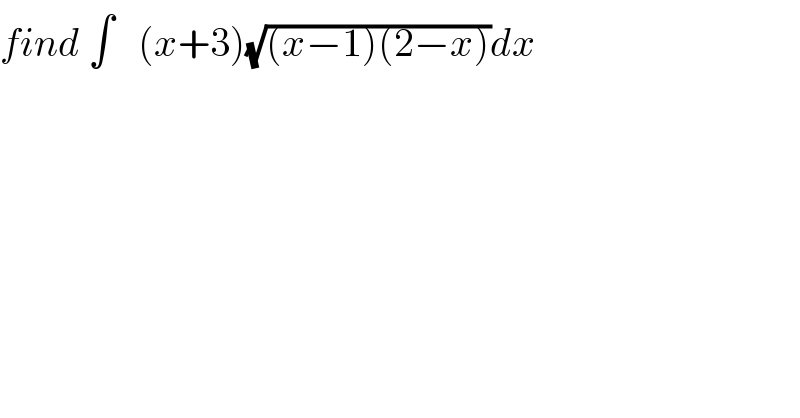
find ∫ (x+3)(√((x−1)(2−x)))dx
$${find}\:\int\:\:\:\left({x}+\mathrm{3}\right)\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}{dx} \\ $$
Commented by mathmax by abdo last updated on 04/Dec/19
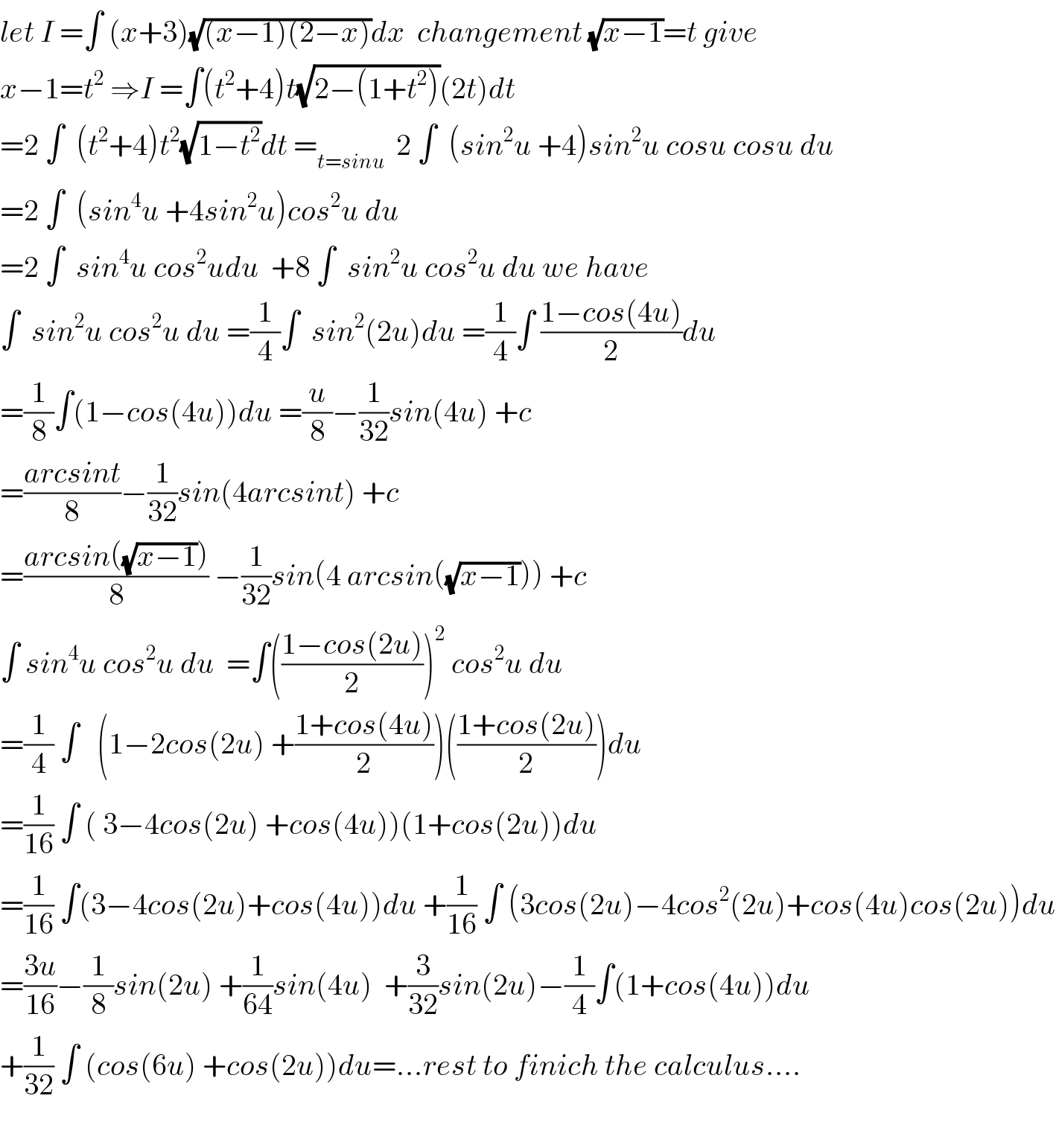
let I =∫ (x+3)(√((x−1)(2−x)))dx changement (√(x−1))=t give x−1=t^2 ⇒I =∫(t^2 +4)t(√(2−(1+t^2 )))(2t)dt =2 ∫ (t^2 +4)t^2 (√(1−t^2 ))dt =_(t=sinu) 2 ∫ (sin^2 u +4)sin^2 u cosu cosu du =2 ∫ (sin^4 u +4sin^2 u)cos^2 u du =2 ∫ sin^4 u cos^2 udu +8 ∫ sin^2 u cos^2 u du we have ∫ sin^2 u cos^2 u du =(1/4)∫ sin^2 (2u)du =(1/4)∫ ((1−cos(4u))/2)du =(1/8)∫(1−cos(4u))du =(u/8)−(1/(32))sin(4u) +c =((arcsint)/8)−(1/(32))sin(4arcsint) +c =((arcsin((√(x−1))))/8) −(1/(32))sin(4 arcsin((√(x−1)))) +c ∫ sin^4 u cos^2 u du =∫(((1−cos(2u))/2))^2 cos^2 u du =(1/4) ∫ (1−2cos(2u) +((1+cos(4u))/2))(((1+cos(2u))/2))du =(1/(16)) ∫ ( 3−4cos(2u) +cos(4u))(1+cos(2u))du =(1/(16)) ∫(3−4cos(2u)+cos(4u))du +(1/(16)) ∫ (3cos(2u)−4cos^2 (2u)+cos(4u)cos(2u))du =((3u)/(16))−(1/8)sin(2u) +(1/(64))sin(4u) +(3/(32))sin(2u)−(1/4)∫(1+cos(4u))du +(1/(32)) ∫ (cos(6u) +cos(2u))du=...rest to finich the calculus....
$${let}\:{I}\:=\int\:\left({x}+\mathrm{3}\right)\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}{dx}\:\:{changement}\:\sqrt{{x}−\mathrm{1}}={t}\:{give} \\ $$$${x}−\mathrm{1}={t}^{\mathrm{2}} \:\Rightarrow{I}\:=\int\left({t}^{\mathrm{2}} +\mathrm{4}\right){t}\sqrt{\mathrm{2}−\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int\:\:\left({t}^{\mathrm{2}} +\mathrm{4}\right){t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:=_{{t}={sinu}} \:\:\mathrm{2}\:\int\:\:\left({sin}^{\mathrm{2}} {u}\:+\mathrm{4}\right){sin}^{\mathrm{2}} {u}\:{cosu}\:{cosu}\:{du} \\ $$$$=\mathrm{2}\:\int\:\:\left({sin}^{\mathrm{4}} {u}\:+\mathrm{4}{sin}^{\mathrm{2}} {u}\right){cos}^{\mathrm{2}} {u}\:{du} \\ $$$$=\mathrm{2}\:\int\:\:{sin}^{\mathrm{4}} {u}\:{cos}^{\mathrm{2}} {udu}\:\:+\mathrm{8}\:\int\:\:{sin}^{\mathrm{2}} {u}\:{cos}^{\mathrm{2}} {u}\:{du}\:{we}\:{have} \\ $$$$\int\:\:{sin}^{\mathrm{2}} {u}\:{cos}^{\mathrm{2}} {u}\:{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:{sin}^{\mathrm{2}} \left(\mathrm{2}{u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{1}−{cos}\left(\mathrm{4}{u}\right)}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\left(\mathrm{1}−{cos}\left(\mathrm{4}{u}\right)\right){du}\:=\frac{{u}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{4}{u}\right)\:+{c} \\ $$$$=\frac{{arcsint}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{4}{arcsint}\right)\:+{c} \\ $$$$=\frac{{arcsin}\left(\sqrt{{x}−\mathrm{1}}\right)}{\mathrm{8}}\:−\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{4}\:{arcsin}\left(\sqrt{{x}−\mathrm{1}}\right)\right)\:+{c} \\ $$$$\int\:{sin}^{\mathrm{4}} {u}\:{cos}^{\mathrm{2}} {u}\:{du}\:\:=\int\left(\frac{\mathrm{1}−{cos}\left(\mathrm{2}{u}\right)}{\mathrm{2}}\right)^{\mathrm{2}} \:{cos}^{\mathrm{2}} {u}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\:\:\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}{u}\right)\:+\frac{\mathrm{1}+{cos}\left(\mathrm{4}{u}\right)}{\mathrm{2}}\right)\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{u}\right)}{\mathrm{2}}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\left(\:\mathrm{3}−\mathrm{4}{cos}\left(\mathrm{2}{u}\right)\:+{cos}\left(\mathrm{4}{u}\right)\right)\left(\mathrm{1}+{cos}\left(\mathrm{2}{u}\right)\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\left(\mathrm{3}−\mathrm{4}{cos}\left(\mathrm{2}{u}\right)+{cos}\left(\mathrm{4}{u}\right)\right){du}\:+\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\left(\mathrm{3}{cos}\left(\mathrm{2}{u}\right)−\mathrm{4}{cos}^{\mathrm{2}} \left(\mathrm{2}{u}\right)+{cos}\left(\mathrm{4}{u}\right){cos}\left(\mathrm{2}{u}\right)\right){du} \\ $$$$=\frac{\mathrm{3}{u}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{8}}{sin}\left(\mathrm{2}{u}\right)\:+\frac{\mathrm{1}}{\mathrm{64}}{sin}\left(\mathrm{4}{u}\right)\:\:+\frac{\mathrm{3}}{\mathrm{32}}{sin}\left(\mathrm{2}{u}\right)−\frac{\mathrm{1}}{\mathrm{4}}\int\left(\mathrm{1}+{cos}\left(\mathrm{4}{u}\right)\right){du} \\ $$$$+\frac{\mathrm{1}}{\mathrm{32}}\:\int\:\left({cos}\left(\mathrm{6}{u}\right)\:+{cos}\left(\mathrm{2}{u}\right)\right){du}=…{rest}\:{to}\:{finich}\:{the}\:{calculus}…. \\ $$$$ \\ $$
Answered by MJS last updated on 03/Dec/19
∫(x+3)(√((x−1)(2−x)))dx= =∫(x+3)(√((1/4)−(x−(3/2))^2 ))dx= [t=2x−3 → dx=(dt/2)] =(1/8)∫(t+9)(√(1−t^2 ))dt= =(1/8)∫t(√(1−t^2 ))dt+(9/8)∫(√(1−t^2 ))dt= [u=arcsin t → dt=(√(1−t^2 ))du] =(1/8)∫sin u cos^2 u du+(9/8)∫cos^2 u du= =−(1/(24))cos^3 u+(9/(16))(u+sin u cos u)= =−(1/(24))(1−t^2 )^(3/2) +(9/(16))t(√(1−t^2 ))+(9/(16))arcsin t = =((1/(24))t^2 +(9/(16))t−(1/(24)))(√(1−t^2 ))+(9/(16))arcsin t = =((1/3)x^2 +(5/4)x−((65)/(24)))(√((x−1)(2−x)))+(9/(16))arcsin (2x−3) +C
$$\int\left({x}+\mathrm{3}\right)\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}{dx}= \\ $$$$=\int\left({x}+\mathrm{3}\right)\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}{x}−\mathrm{3}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\left({t}+\mathrm{9}\right)\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{dt}+\frac{\mathrm{9}}{\mathrm{8}}\int\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{arcsin}\:{t}\:\rightarrow\:{dt}=\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{du}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{sin}\:{u}\:\mathrm{cos}^{\mathrm{2}} \:{u}\:{du}+\frac{\mathrm{9}}{\mathrm{8}}\int\mathrm{cos}^{\mathrm{2}} \:{u}\:{du}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{24}}\mathrm{cos}^{\mathrm{3}} \:{u}+\frac{\mathrm{9}}{\mathrm{16}}\left({u}+\mathrm{sin}\:{u}\:\mathrm{cos}\:{u}\right)= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{24}}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{9}}{\mathrm{16}}{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{16}}\mathrm{arcsin}\:{t}\:= \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{24}}{t}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{16}}{t}−\frac{\mathrm{1}}{\mathrm{24}}\right)\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{16}}\mathrm{arcsin}\:{t}\:= \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{4}}{x}−\frac{\mathrm{65}}{\mathrm{24}}\right)\sqrt{\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right)}+\frac{\mathrm{9}}{\mathrm{16}}\mathrm{arcsin}\:\left(\mathrm{2}{x}−\mathrm{3}\right)\:+{C} \\ $$
Commented by mathmax by abdo last updated on 03/Dec/19
thank you sir mjs
$${thank}\:{you}\:{sir}\:{mjs} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *