Question Number 767 by 123456 last updated on 09/Mar/15
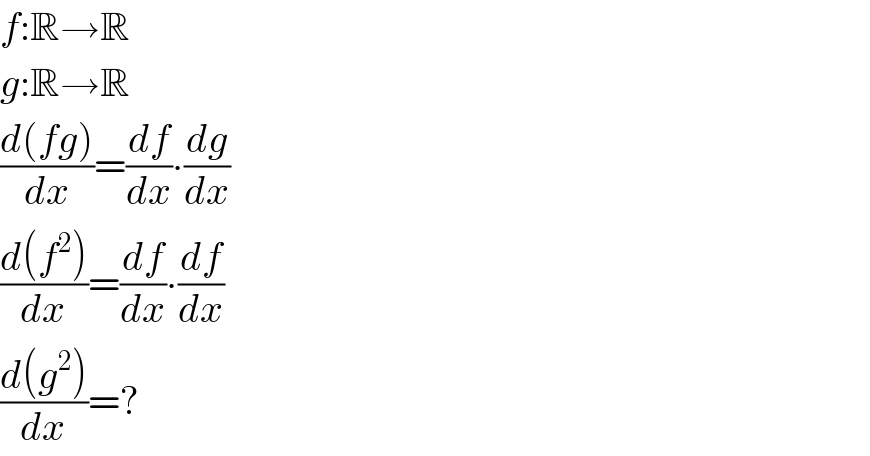
$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${g}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$$\frac{{d}\left({fg}\right)}{{dx}}=\frac{{df}}{{dx}}\centerdot\frac{{dg}}{{dx}} \\ $$$$\frac{{d}\left({f}^{\mathrm{2}} \right)}{{dx}}=\frac{{df}}{{dx}}\centerdot\frac{{df}}{{dx}} \\ $$$$\frac{{d}\left({g}^{\mathrm{2}} \right)}{{dx}}=? \\ $$
Commented by 123456 last updated on 09/Mar/15
![((d(f^2 g^2 ))/dx)=((d(f^2 ))/dx)g^2 +f^2 ((d(g^2 ))/dx)=((df/dx)g)^2 +f^2 ((d(g^2 ))/dx) ((d(f^2 g^2 ))/dx)=2((d(fg))/dx)fg=2(df/dx)∙(dg/dx)fg ((df/dx)g)^2 +f^2 ((d(g^2 ))/dx)=2(df/dx)∙(dg/dx)fg f^2 ((d(g^2 ))/dx)=2(df/dx)∙(dg/dx)fg−((df/dx)g)^2 ((d(g^2 ))/dx)=(1/f^2 )[2(df/dx)∙(dg/dx)fg−((df/dx)g)^2 ] =(1/f^2 )∙(df/dx)g(2(dg/dx)f+(df/dx)g) =(1/f^2 )∙(df/dx)g(f(dg/dx)+f(dg/dx)+(df/dx)g) =(1/f^2 )∙(df/dx)g[f(dg/dx)+((d(fg))/dx)] =(1/f^2 )∙(df/dx)g(f(dg/dx)+(df/dx)∙(dg/dx)) =(1/f^2 )∙(df/dx)∙(dg/dx)g(f+(df/dx))](https://www.tinkutara.com/question/Q768.png)
$$\frac{{d}\left({f}^{\mathrm{2}} {g}^{\mathrm{2}} \right)}{{dx}}=\frac{{d}\left({f}^{\mathrm{2}} \right)}{{dx}}{g}^{\mathrm{2}} +{f}^{\mathrm{2}} \frac{{d}\left({g}^{\mathrm{2}} \right)}{{dx}}=\left(\frac{{df}}{{dx}}{g}\right)^{\mathrm{2}} +{f}^{\mathrm{2}} \frac{{d}\left({g}^{\mathrm{2}} \right)}{{dx}} \\ $$$$\frac{{d}\left({f}^{\mathrm{2}} {g}^{\mathrm{2}} \right)}{{dx}}=\mathrm{2}\frac{{d}\left({fg}\right)}{{dx}}{fg}=\mathrm{2}\frac{{df}}{{dx}}\centerdot\frac{{dg}}{{dx}}{fg} \\ $$$$\left(\frac{{df}}{{dx}}{g}\right)^{\mathrm{2}} +{f}^{\mathrm{2}} \frac{{d}\left({g}^{\mathrm{2}} \right)}{{dx}}=\mathrm{2}\frac{{df}}{{dx}}\centerdot\frac{{dg}}{{dx}}{fg} \\ $$$${f}^{\mathrm{2}} \frac{{d}\left({g}^{\mathrm{2}} \right)}{{dx}}=\mathrm{2}\frac{{df}}{{dx}}\centerdot\frac{{dg}}{{dx}}{fg}−\left(\frac{{df}}{{dx}}{g}\right)^{\mathrm{2}} \\ $$$$\frac{{d}\left({g}^{\mathrm{2}} \right)}{{dx}}=\frac{\mathrm{1}}{{f}^{\mathrm{2}} }\left[\mathrm{2}\frac{{df}}{{dx}}\centerdot\frac{{dg}}{{dx}}{fg}−\left(\frac{{df}}{{dx}}{g}\right)^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{f}^{\mathrm{2}} }\centerdot\frac{{df}}{{dx}}{g}\left(\mathrm{2}\frac{{dg}}{{dx}}{f}+\frac{{df}}{{dx}}{g}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{f}^{\mathrm{2}} }\centerdot\frac{{df}}{{dx}}{g}\left({f}\frac{{dg}}{{dx}}+{f}\frac{{dg}}{{dx}}+\frac{{df}}{{dx}}{g}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{f}^{\mathrm{2}} }\centerdot\frac{{df}}{{dx}}{g}\left[{f}\frac{{dg}}{{dx}}+\frac{{d}\left({fg}\right)}{{dx}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{f}^{\mathrm{2}} }\centerdot\frac{{df}}{{dx}}{g}\left({f}\frac{{dg}}{{dx}}+\frac{{df}}{{dx}}\centerdot\frac{{dg}}{{dx}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{f}^{\mathrm{2}} }\centerdot\frac{{df}}{{dx}}\centerdot\frac{{dg}}{{dx}}{g}\left({f}+\frac{{df}}{{dx}}\right) \\ $$
