Question Number 66304 by mathmax by abdo last updated on 12/Aug/19
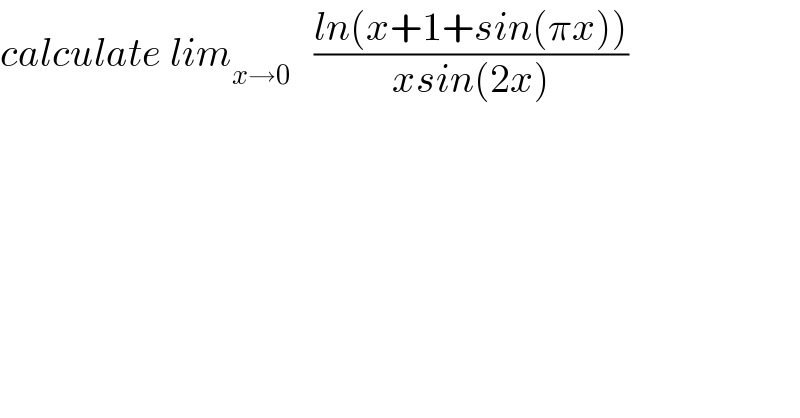
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{ln}\left({x}+\mathrm{1}+{sin}\left(\pi{x}\right)\right)}{{xsin}\left(\mathrm{2}{x}\right)} \\ $$
Answered by kaivan.ahmadi last updated on 12/Aug/19
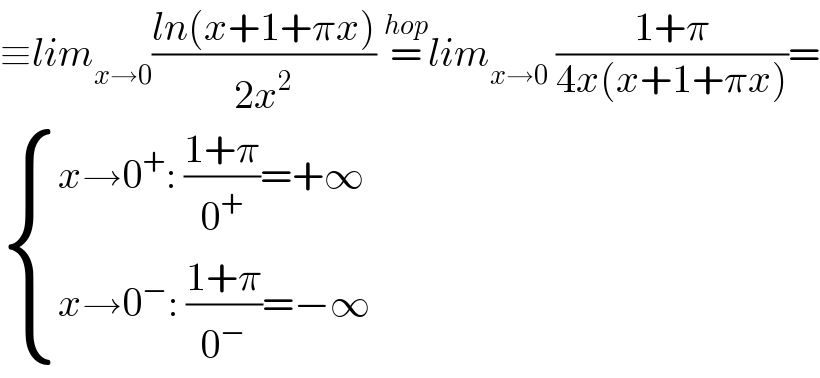
$$\equiv{lim}_{{x}\rightarrow\mathrm{0}} \frac{{ln}\left({x}+\mathrm{1}+\pi{x}\right)}{\mathrm{2}{x}^{\mathrm{2}} }\:\overset{{hop}} {=}{lim}_{{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}+\pi}{\mathrm{4}{x}\left({x}+\mathrm{1}+\pi{x}\right)}= \\ $$$$\begin{cases}{{x}\rightarrow\mathrm{0}^{+} :\:\frac{\mathrm{1}+\pi}{\mathrm{0}^{+} }=+\infty}\\{{x}\rightarrow\mathrm{0}^{−} :\:\frac{\mathrm{1}+\pi}{\mathrm{0}^{−} }=−\infty}\end{cases} \\ $$
