Menu Close

Question-66310

Tinku Tara 0 Comments
Pin




Question Number 66310 by mr W last updated on 12/Aug/19
Commented by mr W last updated on 12/Aug/19
all contact is frictionless. find the minimum length of uniform rope such that it can stay in equilibrium as shown.
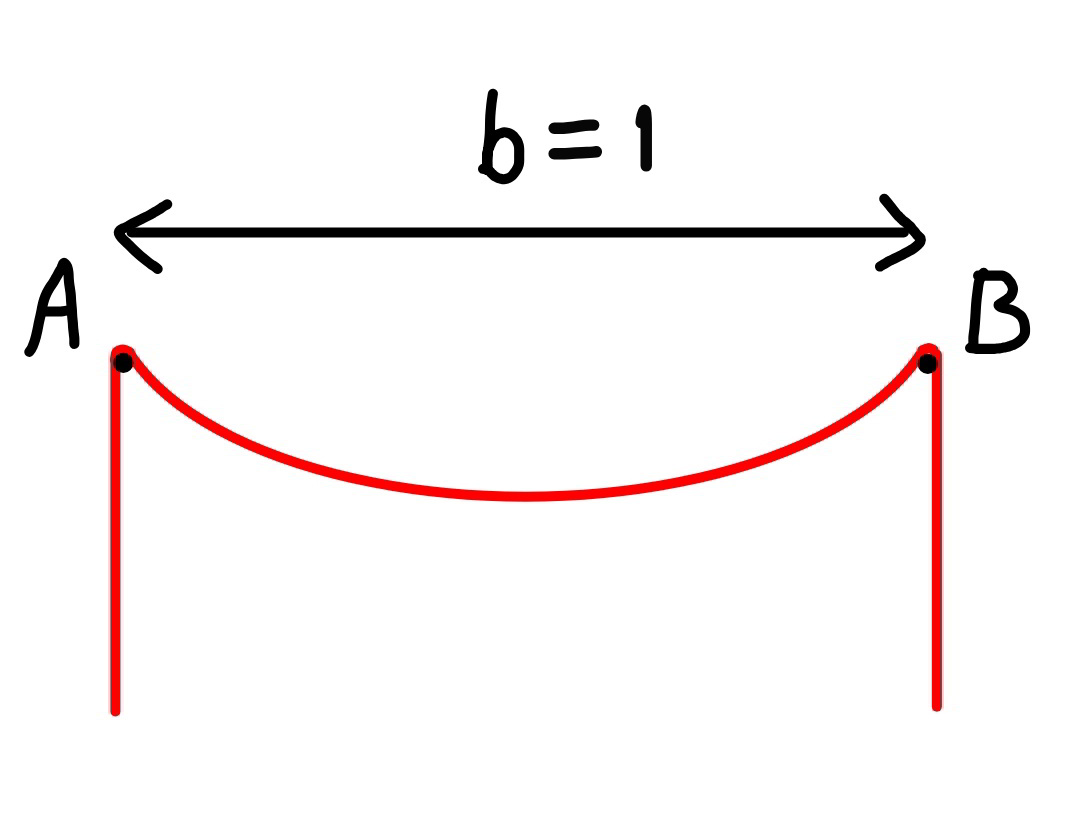
$${all}\:{contact}\:{is}\:{frictionless}. \\ $$$${find}\:{the}\:{minimum}\:{length}\:{of}\:{uniform} \\ $$$${rope}\:{such}\:{that}\:{it}\:{can}\:{stay}\:{in}\:{equilibrium} \\ $$$${as}\:{shown}. \\ $$
Answered by mr W last updated on 13/Aug/19
Commented by mr W last updated on 14/Aug/19
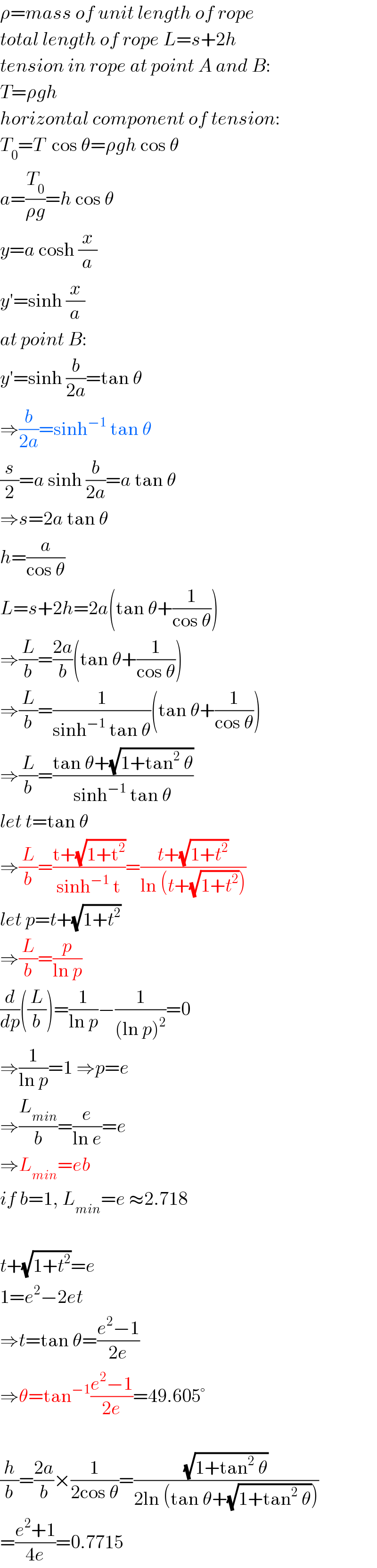
ρ=mass of unit length of rope total length of rope L=s+2h tension in rope at point A and B: T=ρgh horizontal component of tension: T_0 =T cos θ=ρgh cos θ a=(T_0 /(ρg))=h cos θ y=a cosh (x/a) y′=sinh (x/a) at point B: y′=sinh (b/(2a))=tan θ ⇒(b/(2a))=sinh^(−1) tan θ (s/2)=a sinh (b/(2a))=a tan θ ⇒s=2a tan θ h=(a/(cos θ)) L=s+2h=2a(tan θ+(1/(cos θ))) ⇒(L/b)=((2a)/b)(tan θ+(1/(cos θ))) ⇒(L/b)=(1/(sinh^(−1) tan θ))(tan θ+(1/(cos θ))) ⇒(L/b)=((tan θ+(√(1+tan^2 θ)))/(sinh^(−1) tan θ)) let t=tan θ ⇒(L/b)=((t+(√(1+t^2 )))/(sinh^(−1) t))=((t+(√(1+t^2 )))/(ln (t+(√(1+t^2 ))))) let p=t+(√(1+t^2 )) ⇒(L/b)=(p/(ln p)) (d/dp)((L/b))=(1/(ln p))−(1/((ln p)^2 ))=0 ⇒(1/(ln p))=1 ⇒p=e ⇒(L_(min) /b)=(e/(ln e))=e ⇒L_(min) =eb if b=1, L_(min) =e ≈2.718 t+(√(1+t^2 ))=e 1=e^2 −2et ⇒t=tan θ=((e^2 −1)/(2e)) ⇒θ=tan^(−1) ((e^2 −1)/(2e))=49.605° (h/b)=((2a)/b)×(1/(2cos θ))=((√(1+tan^2 θ))/(2ln (tan θ+(√(1+tan^2 θ))))) =((e^2 +1)/(4e))=0.7715
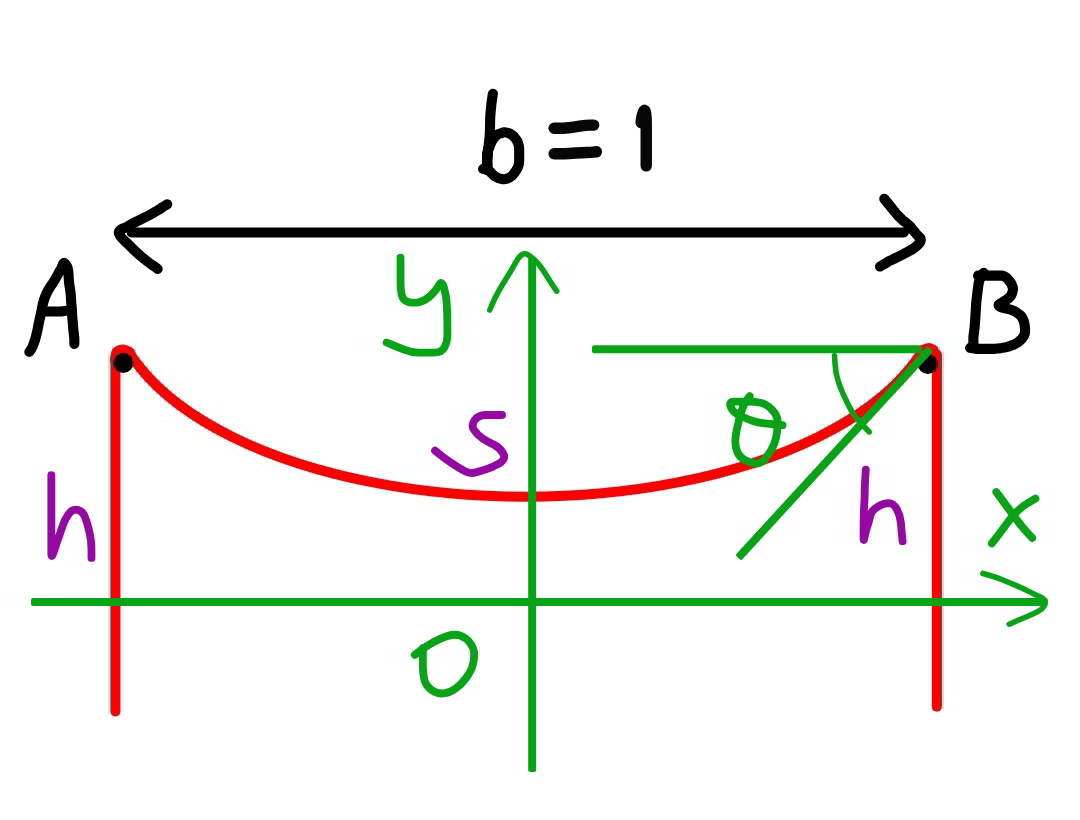
$$\rho={mass}\:{of}\:{unit}\:{length}\:{of}\:{rope} \\ $$$${total}\:{length}\:{of}\:{rope}\:{L}={s}+\mathrm{2}{h} \\ $$$${tension}\:{in}\:{rope}\:{at}\:{point}\:{A}\:{and}\:{B}: \\ $$$${T}=\rho{gh} \\ $$$${horizontal}\:{component}\:{of}\:{tension}: \\ $$$${T}_{\mathrm{0}} ={T}\:\:\mathrm{cos}\:\theta=\rho{gh}\:\mathrm{cos}\:\theta \\ $$$${a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}={h}\:\mathrm{cos}\:\theta \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${at}\:{point}\:{B}: \\ $$$${y}'=\mathrm{sinh}\:\frac{{b}}{\mathrm{2}{a}}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\frac{{b}}{\mathrm{2}{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\mathrm{tan}\:\theta \\ $$$$\frac{{s}}{\mathrm{2}}={a}\:\mathrm{sinh}\:\frac{{b}}{\mathrm{2}{a}}={a}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{s}=\mathrm{2}{a}\:\mathrm{tan}\:\theta \\ $$$${h}=\frac{{a}}{\mathrm{cos}\:\theta} \\ $$$${L}={s}+\mathrm{2}{h}=\mathrm{2}{a}\left(\mathrm{tan}\:\theta+\frac{\mathrm{1}}{\mathrm{cos}\:\theta}\right) \\ $$$$\Rightarrow\frac{{L}}{{b}}=\frac{\mathrm{2}{a}}{{b}}\left(\mathrm{tan}\:\theta+\frac{\mathrm{1}}{\mathrm{cos}\:\theta}\right) \\ $$$$\Rightarrow\frac{{L}}{{b}}=\frac{\mathrm{1}}{\mathrm{sinh}^{−\mathrm{1}} \:\mathrm{tan}\:\theta}\left(\mathrm{tan}\:\theta+\frac{\mathrm{1}}{\mathrm{cos}\:\theta}\right) \\ $$$$\Rightarrow\frac{{L}}{{b}}=\frac{\mathrm{tan}\:\theta+\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}}{\mathrm{sinh}^{−\mathrm{1}} \:\mathrm{tan}\:\theta} \\ $$$${let}\:{t}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\frac{{L}}{{b}}=\frac{\mathrm{t}+\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{sinh}^{−\mathrm{1}} \:\mathrm{t}}=\frac{{t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{ln}\:\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$${let}\:{p}={t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{L}}{{b}}=\frac{{p}}{\mathrm{ln}\:{p}} \\ $$$$\frac{{d}}{{dp}}\left(\frac{{L}}{{b}}\right)=\frac{\mathrm{1}}{\mathrm{ln}\:{p}}−\frac{\mathrm{1}}{\left(\mathrm{ln}\:{p}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{ln}\:{p}}=\mathrm{1}\:\Rightarrow{p}={e} \\ $$$$\Rightarrow\frac{{L}_{{min}} }{{b}}=\frac{{e}}{\mathrm{ln}\:{e}}={e} \\ $$$$\Rightarrow{L}_{{min}} ={eb} \\ $$$${if}\:{b}=\mathrm{1},\:{L}_{{min}} ={e}\:\approx\mathrm{2}.\mathrm{718} \\ $$$$ \\ $$$${t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }={e} \\ $$$$\mathrm{1}={e}^{\mathrm{2}} −\mathrm{2}{et} \\ $$$$\Rightarrow{t}=\mathrm{tan}\:\theta=\frac{{e}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{e}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{{e}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{e}}=\mathrm{49}.\mathrm{605}° \\ $$$$ \\ $$$$\frac{{h}}{{b}}=\frac{\mathrm{2}{a}}{{b}}×\frac{\mathrm{1}}{\mathrm{2cos}\:\theta}=\frac{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}}{\mathrm{2ln}\:\left(\mathrm{tan}\:\theta+\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}\right)} \\ $$$$=\frac{{e}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}{e}}=\mathrm{0}.\mathrm{7715} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *