Question Number 75048 by mathocean1 last updated on 06/Dec/19
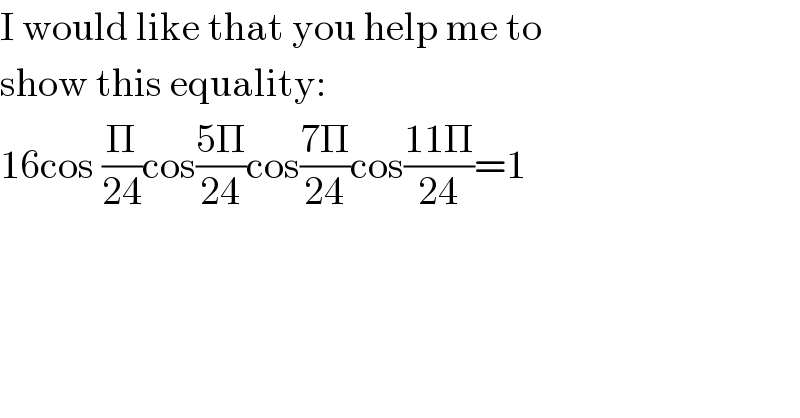
$$\mathrm{I}\:\mathrm{would}\:\mathrm{like}\:\mathrm{that}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}\:\mathrm{to}\: \\ $$$$\mathrm{show}\:\mathrm{this}\:\mathrm{equality}: \\ $$$$\mathrm{16cos}\:\frac{\Pi}{\mathrm{24}}\mathrm{cos}\frac{\mathrm{5}\Pi}{\mathrm{24}}\mathrm{cos}\frac{\mathrm{7}\Pi}{\mathrm{24}}\mathrm{cos}\frac{\mathrm{11}\Pi}{\mathrm{24}}=\mathrm{1} \\ $$
Commented by mind is power last updated on 06/Dec/19
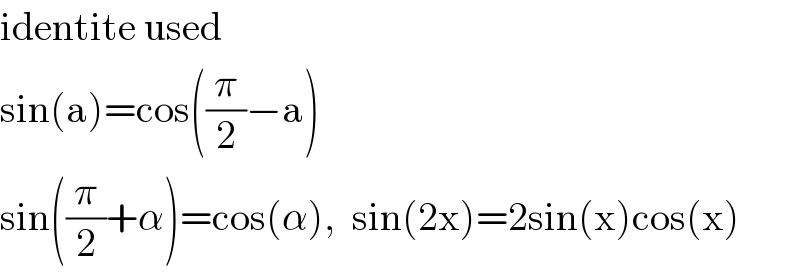
$$\mathrm{identite}\:\mathrm{used} \\ $$$$\mathrm{sin}\left(\mathrm{a}\right)=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{a}\right) \\ $$$$\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}+\alpha\right)=\mathrm{cos}\left(\alpha\right),\:\:\mathrm{sin}\left(\mathrm{2x}\right)=\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right) \\ $$
Answered by mind is power last updated on 06/Dec/19
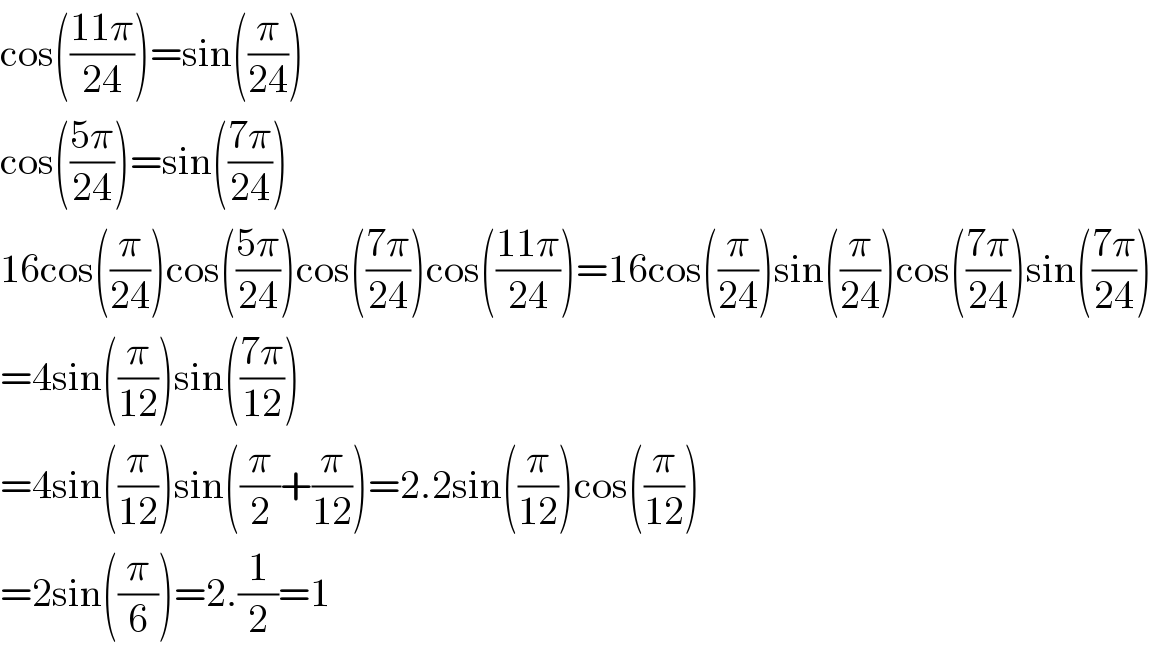
$$\mathrm{cos}\left(\frac{\mathrm{11}\pi}{\mathrm{24}}\right)=\mathrm{sin}\left(\frac{\pi}{\mathrm{24}}\right) \\ $$$$\mathrm{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{24}}\right)=\mathrm{sin}\left(\frac{\mathrm{7}\pi}{\mathrm{24}}\right) \\ $$$$\mathrm{16cos}\left(\frac{\pi}{\mathrm{24}}\right)\mathrm{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{24}}\right)\mathrm{cos}\left(\frac{\mathrm{7}\pi}{\mathrm{24}}\right)\mathrm{cos}\left(\frac{\mathrm{11}\pi}{\mathrm{24}}\right)=\mathrm{16cos}\left(\frac{\pi}{\mathrm{24}}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{24}}\right)\mathrm{cos}\left(\frac{\mathrm{7}\pi}{\mathrm{24}}\right)\mathrm{sin}\left(\frac{\mathrm{7}\pi}{\mathrm{24}}\right) \\ $$$$=\mathrm{4sin}\left(\frac{\pi}{\mathrm{12}}\right)\mathrm{sin}\left(\frac{\mathrm{7}\pi}{\mathrm{12}}\right) \\ $$$$=\mathrm{4sin}\left(\frac{\pi}{\mathrm{12}}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{12}}\right)=\mathrm{2}.\mathrm{2sin}\left(\frac{\pi}{\mathrm{12}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{12}}\right) \\ $$$$=\mathrm{2sin}\left(\frac{\pi}{\mathrm{6}}\right)=\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{1} \\ $$
Commented by mathocean1 last updated on 06/Dec/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}! \\ $$
Commented by peter frank last updated on 06/Dec/19

$${thank}\:{you} \\ $$
Commented by peter frank last updated on 06/Dec/19

$${thank}\:{you} \\ $$
