Question Number 140589 by bramlexs22 last updated on 09/May/21
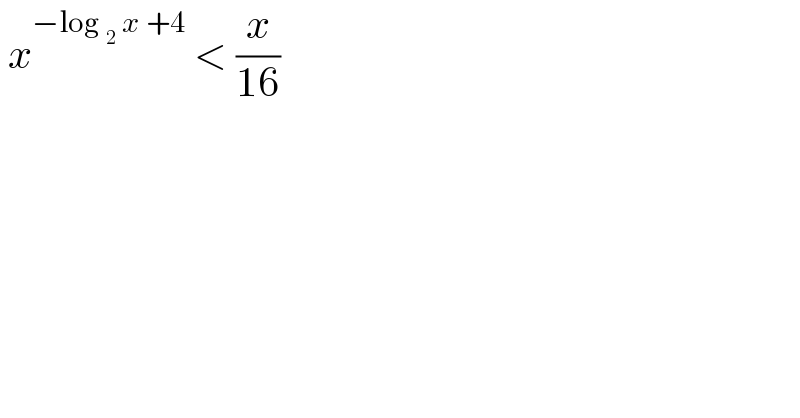
$$\:{x}^{−\mathrm{log}\:_{\mathrm{2}} \:{x}\:+\mathrm{4}} \:<\:\frac{{x}}{\mathrm{16}} \\ $$
Answered by MJS_new last updated on 10/May/21
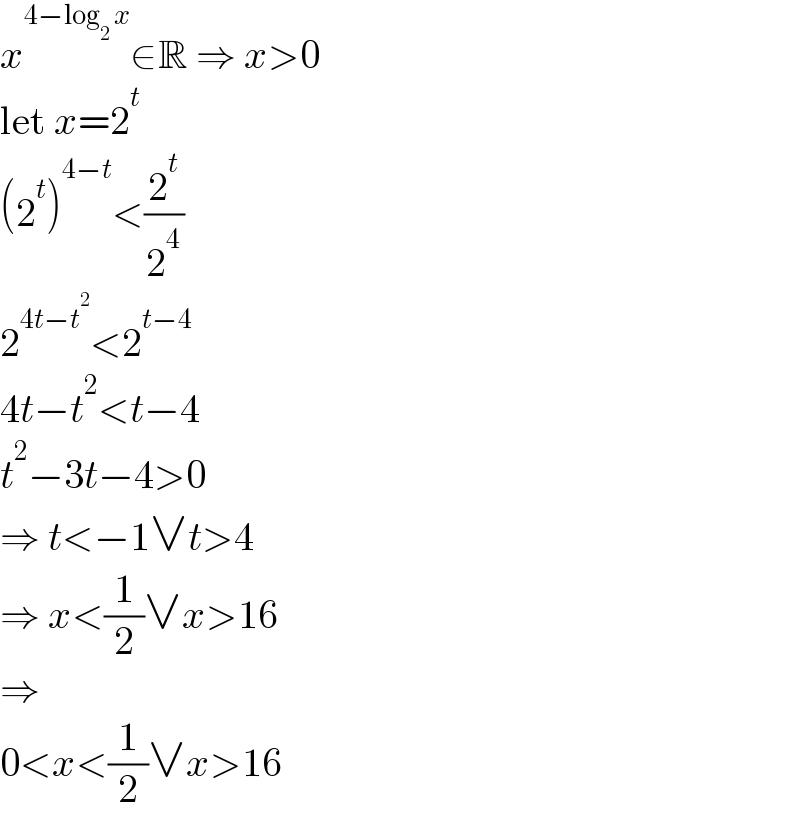
$${x}^{\mathrm{4}−\mathrm{log}_{\mathrm{2}} \:{x}} \in\mathbb{R}\:\Rightarrow\:{x}>\mathrm{0} \\ $$$$\mathrm{let}\:{x}=\mathrm{2}^{{t}} \\ $$$$\left(\mathrm{2}^{{t}} \right)^{\mathrm{4}−{t}} <\frac{\mathrm{2}^{{t}} }{\mathrm{2}^{\mathrm{4}} } \\ $$$$\mathrm{2}^{\mathrm{4}{t}−{t}^{\mathrm{2}} } <\mathrm{2}^{{t}−\mathrm{4}} \\ $$$$\mathrm{4}{t}−{t}^{\mathrm{2}} <{t}−\mathrm{4} \\ $$$${t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{4}>\mathrm{0} \\ $$$$\Rightarrow\:{t}<−\mathrm{1}\vee{t}>\mathrm{4} \\ $$$$\Rightarrow\:{x}<\frac{\mathrm{1}}{\mathrm{2}}\vee{x}>\mathrm{16} \\ $$$$\Rightarrow \\ $$$$\mathrm{0}<{x}<\frac{\mathrm{1}}{\mathrm{2}}\vee{x}>\mathrm{16} \\ $$
Commented by bramlexs22 last updated on 10/May/21

$$\mathrm{nice}\:\mathrm{sir} \\ $$
Answered by bemath last updated on 10/May/21
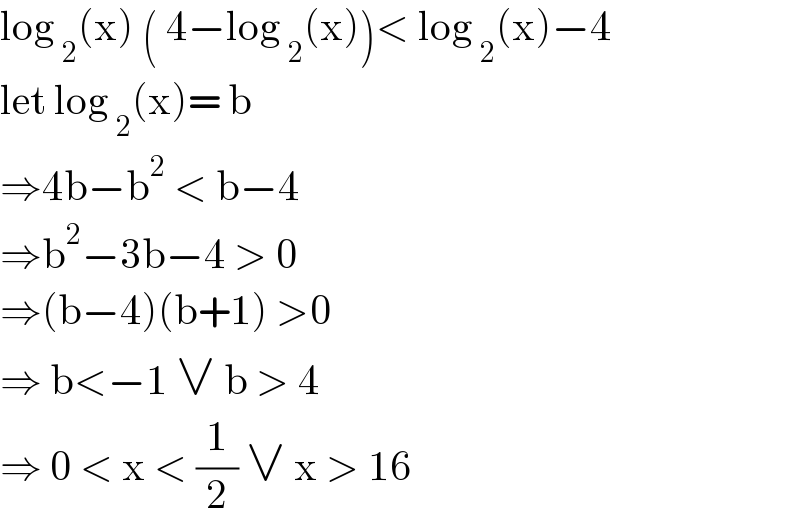
$$\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{x}\right)\:\left(\:\mathrm{4}−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{x}\right)\right)<\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{4} \\ $$$$\mathrm{let}\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{x}\right)=\:\mathrm{b} \\ $$$$\Rightarrow\mathrm{4b}−\mathrm{b}^{\mathrm{2}} \:<\:\mathrm{b}−\mathrm{4}\: \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} −\mathrm{3b}−\mathrm{4}\:>\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{b}−\mathrm{4}\right)\left(\mathrm{b}+\mathrm{1}\right)\:>\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{b}<−\mathrm{1}\:\vee\:\mathrm{b}\:>\:\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{0}\:<\:\mathrm{x}\:<\:\frac{\mathrm{1}}{\mathrm{2}}\:\vee\:\mathrm{x}\:>\:\mathrm{16}\: \\ $$
