Question Number 66316 by mathmax by abdo last updated on 12/Aug/19
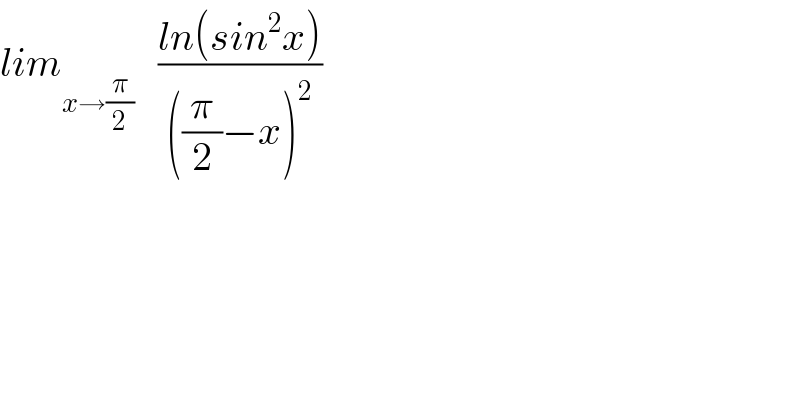
$${lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{ln}\left({sin}^{\mathrm{2}} {x}\right)}{\left(\frac{\pi}{\mathrm{2}}−{x}\right)^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 21/Aug/19
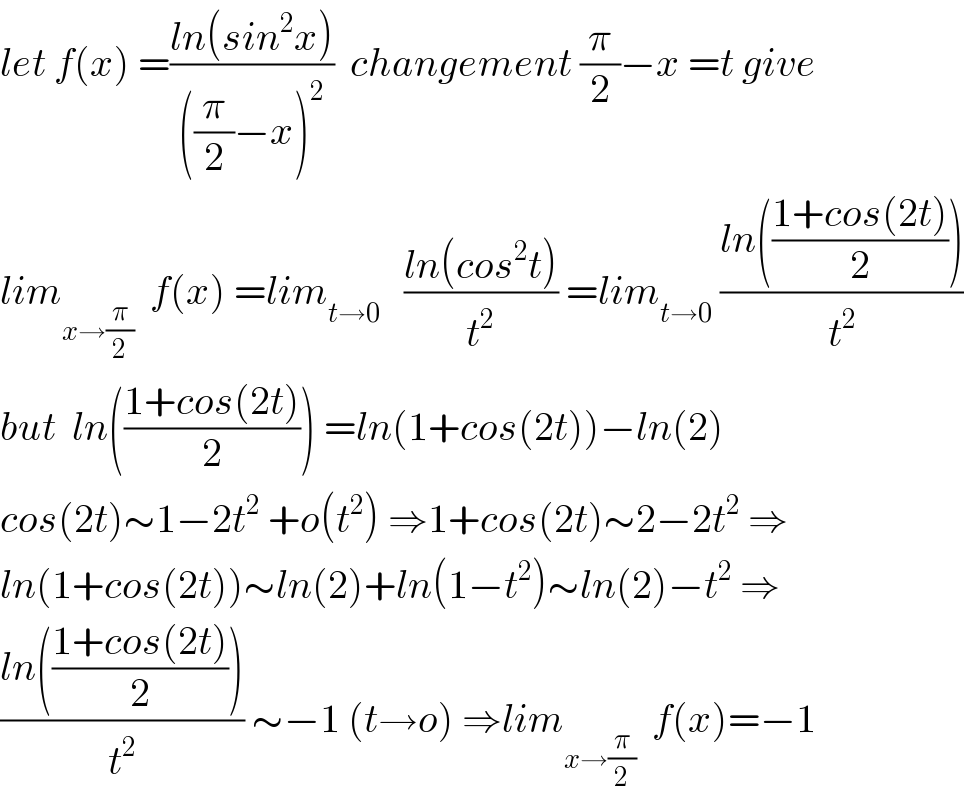
$${let}\:{f}\left({x}\right)\:=\frac{{ln}\left({sin}^{\mathrm{2}} {x}\right)}{\left(\frac{\pi}{\mathrm{2}}−{x}\right)^{\mathrm{2}} }\:\:{changement}\:\frac{\pi}{\mathrm{2}}−{x}\:={t}\:{give} \\ $$$${lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:{f}\left({x}\right)\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{{ln}\left({cos}^{\mathrm{2}} {t}\right)}{{t}^{\mathrm{2}} }\:={lim}_{{t}\rightarrow\mathrm{0}} \:\frac{{ln}\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)}{{t}^{\mathrm{2}} } \\ $$$${but}\:\:{ln}\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)\:={ln}\left(\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\right)−{ln}\left(\mathrm{2}\right) \\ $$$${cos}\left(\mathrm{2}{t}\right)\sim\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \:+{o}\left({t}^{\mathrm{2}} \right)\:\Rightarrow\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\sim\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\right)\sim{ln}\left(\mathrm{2}\right)+{ln}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\sim{ln}\left(\mathrm{2}\right)−{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\frac{{ln}\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)}{{t}^{\mathrm{2}} }\:\sim−\mathrm{1}\:\left({t}\rightarrow{o}\right)\:\Rightarrow{lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:{f}\left({x}\right)=−\mathrm{1} \\ $$
Answered by kaivan.ahmadi last updated on 12/Aug/19
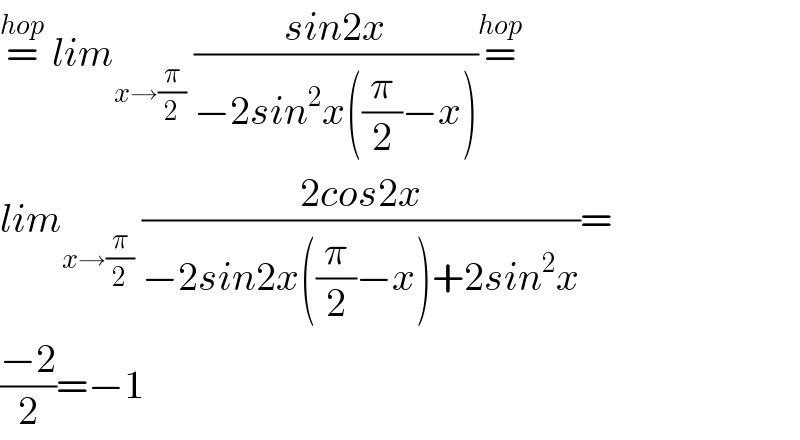
$$\overset{{hop}} {=}\:{lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\mathrm{2}{x}}{−\mathrm{2}{sin}^{\mathrm{2}} {x}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}\overset{{hop}} {=} \\ $$$${lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{2}{cos}\mathrm{2}{x}}{−\mathrm{2}{sin}\mathrm{2}{x}\left(\frac{\pi}{\mathrm{2}}−{x}\right)+\mathrm{2}{sin}^{\mathrm{2}} {x}}= \\ $$$$\frac{−\mathrm{2}}{\mathrm{2}}=−\mathrm{1} \\ $$
