Menu Close

Find-th-greatest-coefficients-in-the-expansion-of-3a-5b-18-2-If-three-consecutive-coefficient-of-1-x-n-are-28-56-70-find-the-value-of-n-

Tinku Tara 0 Comments
Pin




Question Number 75242 by peter frank last updated on 08/Dec/19
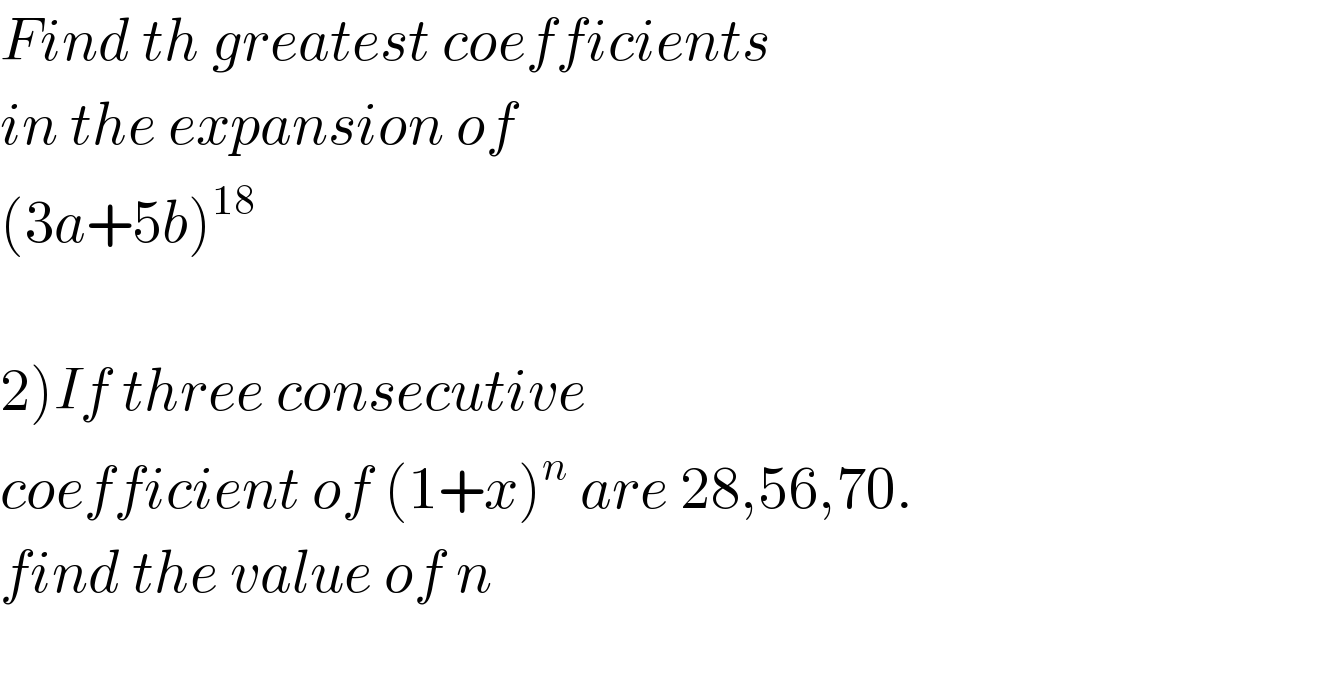
Find th greatest coefficients in the expansion of (3a+5b)^(18) 2)If three consecutive coefficient of (1+x)^n are 28,56,70. find the value of n
$${Find}\:{th}\:{greatest}\:{coefficients} \\ $$$${in}\:{the}\:{expansion}\:{of} \\ $$$$\left(\mathrm{3}{a}+\mathrm{5}{b}\right)^{\mathrm{18}} \\ $$$$ \\ $$$$\left.\mathrm{2}\right){If}\:{three}\:{consecutive}\: \\ $$$${coefficient}\:{of}\:\left(\mathrm{1}+{x}\right)^{{n}} \:{are}\:\mathrm{28},\mathrm{56},\mathrm{70}. \\ $$$${find}\:{the}\:{value}\:{of}\:{n} \\ $$$$ \\ $$
Answered by mr W last updated on 08/Dec/19
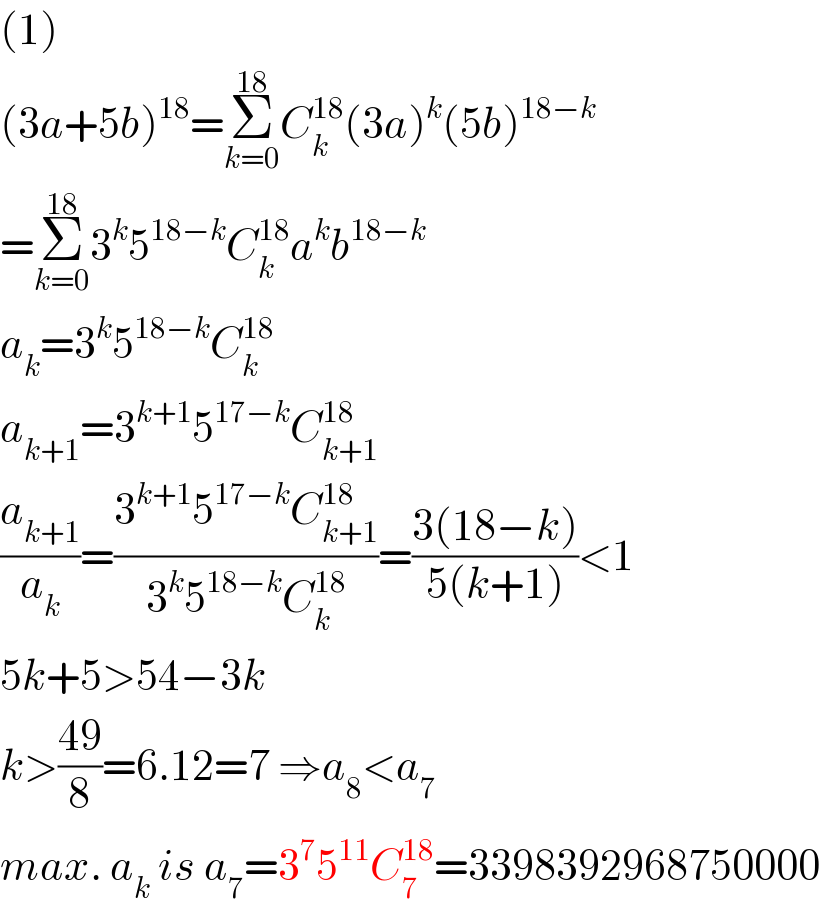
(1) (3a+5b)^(18) =Σ_(k=0) ^(18) C_k ^(18) (3a)^k (5b)^(18−k) =Σ_(k=0) ^(18) 3^k 5^(18−k) C_k ^(18) a^k b^(18−k) a_k =3^k 5^(18−k) C_k ^(18) a_(k+1) =3^(k+1) 5^(17−k) C_(k+1) ^(18) (a_(k+1) /a_k )=((3^(k+1) 5^(17−k) C_(k+1) ^(18) )/(3^k 5^(18−k) C_k ^(18) ))=((3(18−k))/(5(k+1)))<1 5k+5>54−3k k>((49)/8)=6.12=7 ⇒a_8 <a_7 max. a_k is a_7 =3^7 5^(11) C_7 ^(18) =3398392968750000
$$\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{3}{a}+\mathrm{5}{b}\right)^{\mathrm{18}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{18}} {\sum}}{C}_{{k}} ^{\mathrm{18}} \left(\mathrm{3}{a}\right)^{{k}} \left(\mathrm{5}{b}\right)^{\mathrm{18}−{k}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{18}} {\sum}}\mathrm{3}^{{k}} \mathrm{5}^{\mathrm{18}−{k}} {C}_{{k}} ^{\mathrm{18}} {a}^{{k}} {b}^{\mathrm{18}−{k}} \\ $$$${a}_{{k}} =\mathrm{3}^{{k}} \mathrm{5}^{\mathrm{18}−{k}} {C}_{{k}} ^{\mathrm{18}} \\ $$$${a}_{{k}+\mathrm{1}} =\mathrm{3}^{{k}+\mathrm{1}} \mathrm{5}^{\mathrm{17}−{k}} {C}_{{k}+\mathrm{1}} ^{\mathrm{18}} \\ $$$$\frac{{a}_{{k}+\mathrm{1}} }{{a}_{{k}} }=\frac{\mathrm{3}^{{k}+\mathrm{1}} \mathrm{5}^{\mathrm{17}−{k}} {C}_{{k}+\mathrm{1}} ^{\mathrm{18}} }{\mathrm{3}^{{k}} \mathrm{5}^{\mathrm{18}−{k}} {C}_{{k}} ^{\mathrm{18}} }=\frac{\mathrm{3}\left(\mathrm{18}−{k}\right)}{\mathrm{5}\left({k}+\mathrm{1}\right)}<\mathrm{1} \\ $$$$\mathrm{5}{k}+\mathrm{5}>\mathrm{54}−\mathrm{3}{k} \\ $$$${k}>\frac{\mathrm{49}}{\mathrm{8}}=\mathrm{6}.\mathrm{12}=\mathrm{7}\:\Rightarrow{a}_{\mathrm{8}} <{a}_{\mathrm{7}} \\ $$$${max}.\:{a}_{{k}} \:{is}\:{a}_{\mathrm{7}} =\mathrm{3}^{\mathrm{7}} \mathrm{5}^{\mathrm{11}} {C}_{\mathrm{7}} ^{\mathrm{18}} =\mathrm{3398392968750000} \\ $$
Commented by peter frank last updated on 09/Dec/19
thank you very much
$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by mr W last updated on 08/Dec/19
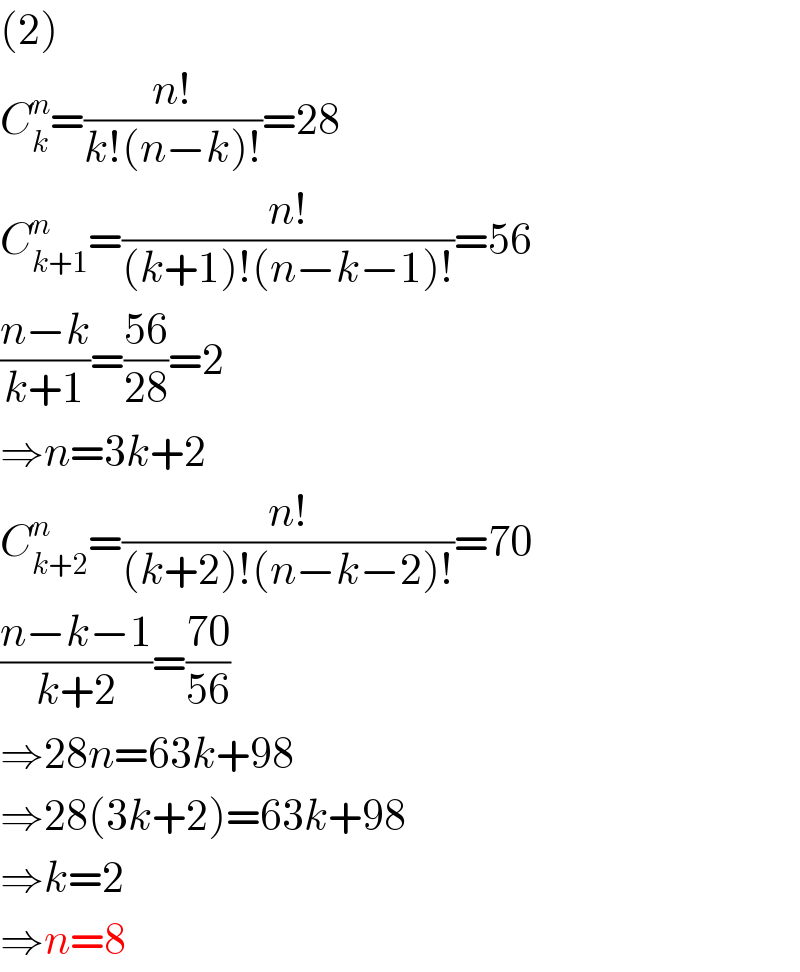
(2) C_k ^n =((n!)/(k!(n−k)!))=28 C_(k+1) ^n =((n!)/((k+1)!(n−k−1)!))=56 ((n−k)/(k+1))=((56)/(28))=2 ⇒n=3k+2 C_(k+2) ^n =((n!)/((k+2)!(n−k−2)!))=70 ((n−k−1)/(k+2))=((70)/(56)) ⇒28n=63k+98 ⇒28(3k+2)=63k+98 ⇒k=2 ⇒n=8
$$\left(\mathrm{2}\right) \\ $$$${C}_{{k}} ^{{n}} =\frac{{n}!}{{k}!\left({n}−{k}\right)!}=\mathrm{28} \\ $$$${C}_{{k}+\mathrm{1}} ^{{n}} =\frac{{n}!}{\left({k}+\mathrm{1}\right)!\left({n}−{k}−\mathrm{1}\right)!}=\mathrm{56} \\ $$$$\frac{{n}−{k}}{{k}+\mathrm{1}}=\frac{\mathrm{56}}{\mathrm{28}}=\mathrm{2} \\ $$$$\Rightarrow{n}=\mathrm{3}{k}+\mathrm{2} \\ $$$${C}_{{k}+\mathrm{2}} ^{{n}} =\frac{{n}!}{\left({k}+\mathrm{2}\right)!\left({n}−{k}−\mathrm{2}\right)!}=\mathrm{70} \\ $$$$\frac{{n}−{k}−\mathrm{1}}{{k}+\mathrm{2}}=\frac{\mathrm{70}}{\mathrm{56}} \\ $$$$\Rightarrow\mathrm{28}{n}=\mathrm{63}{k}+\mathrm{98} \\ $$$$\Rightarrow\mathrm{28}\left(\mathrm{3}{k}+\mathrm{2}\right)=\mathrm{63}{k}+\mathrm{98} \\ $$$$\Rightarrow{k}=\mathrm{2} \\ $$$$\Rightarrow{n}=\mathrm{8} \\ $$
Commented by peter frank last updated on 09/Dec/19
thank you very much
$${thank}\:{you}\:{very}\:{much} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *