Question Number 75577 by Tony Lin last updated on 13/Dec/19
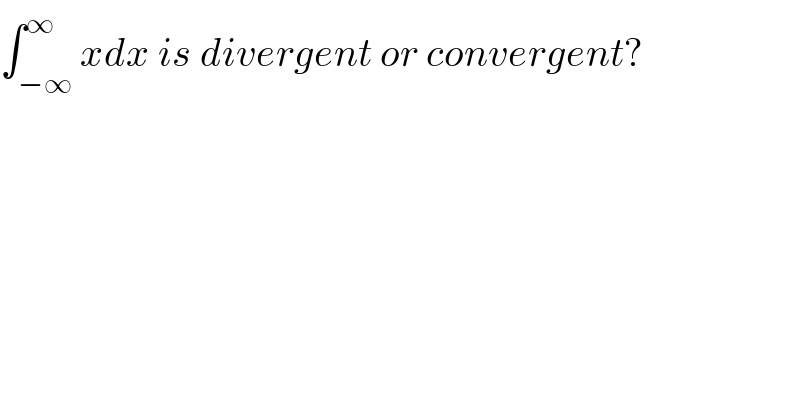
$$\int_{−\infty} ^{\infty} {xdx}\:{is}\:{divergent}\:{or}\:{convergent}? \\ $$
Answered by MJS last updated on 13/Dec/19
![∫_(−∞) ^(+∞) xdx=lim_(r→∞) (∫_(−r) ^r xdx) =lim_(r→∞) ([(x^2 /2)]_(−r) ^r ) =lim_(r→∞) 0 =0](https://www.tinkutara.com/question/Q75582.png)
$$\underset{−\infty} {\overset{+\infty} {\int}}{xdx}=\underset{{r}\rightarrow\infty} {\mathrm{lim}}\left(\underset{−{r}} {\overset{{r}} {\int}}{xdx}\right)\:=\underset{{r}\rightarrow\infty} {\mathrm{lim}}\left(\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{−{r}} ^{{r}} \right)\:=\underset{{r}\rightarrow\infty} {\mathrm{lim}0}\:=\mathrm{0} \\ $$
Commented by MJS last updated on 13/Dec/19

$$\mathrm{no} \\ $$
Commented by Tony Lin last updated on 13/Dec/19
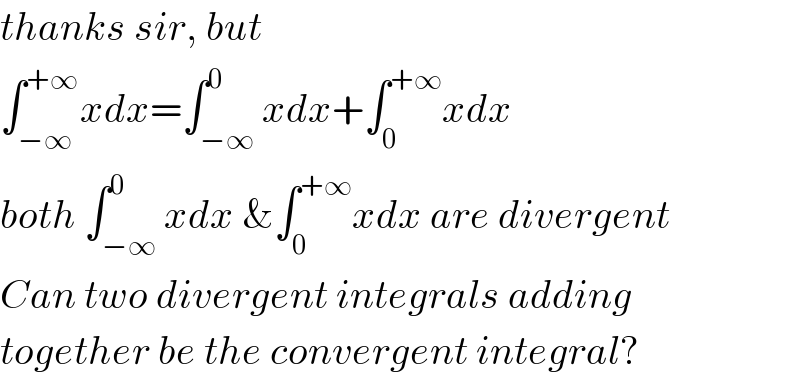
$${thanks}\:{sir},\:{but}\: \\ $$$$\int_{−\infty} ^{+\infty} {xdx}=\int_{−\infty} ^{\mathrm{0}} {xdx}+\int_{\mathrm{0}} ^{+\infty} {xdx} \\ $$$${both}\:\int_{−\infty} ^{\mathrm{0}} {xdx}\:\&\int_{\mathrm{0}} ^{+\infty} {xdx}\:{are}\:{divergent} \\ $$$${Can}\:{two}\:{divergent}\:{integrals}\:{adding} \\ $$$${together}\:{be}\:{the}\:{convergent}\:{integral}? \\ $$
Commented by MJS last updated on 13/Dec/19
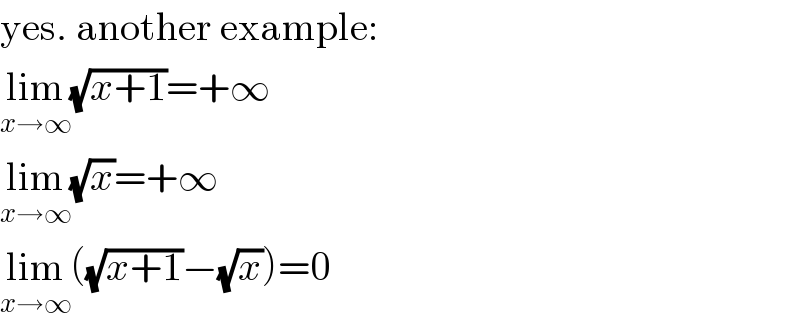
$$\mathrm{yes}.\:\mathrm{another}\:\mathrm{example}: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{{x}+\mathrm{1}}=+\infty \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{{x}}=+\infty \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}}\right)=\mathrm{0} \\ $$
Commented by vishalbhardwaj last updated on 13/Dec/19
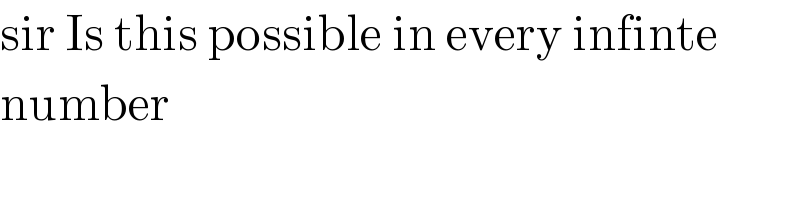
$$\mathrm{sir}\:\mathrm{Is}\:\mathrm{this}\:\mathrm{possible}\:\mathrm{in}\:\mathrm{every}\:\mathrm{infinte} \\ $$$$\mathrm{number} \\ $$
Commented by vishalbhardwaj last updated on 13/Dec/19
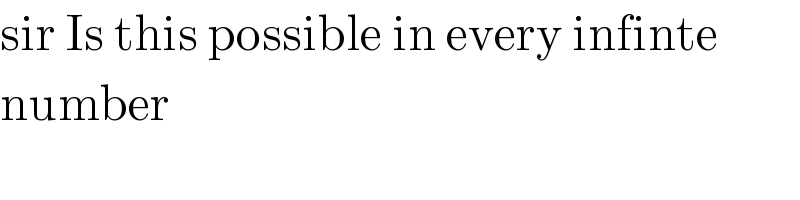
$$\mathrm{sir}\:\mathrm{Is}\:\mathrm{this}\:\mathrm{possible}\:\mathrm{in}\:\mathrm{every}\:\mathrm{infinte} \\ $$$$\mathrm{number} \\ $$
Commented by Tony Lin last updated on 14/Dec/19

$${thanks}\:{sir} \\ $$
