Question Number 75639 by aliesam last updated on 14/Dec/19
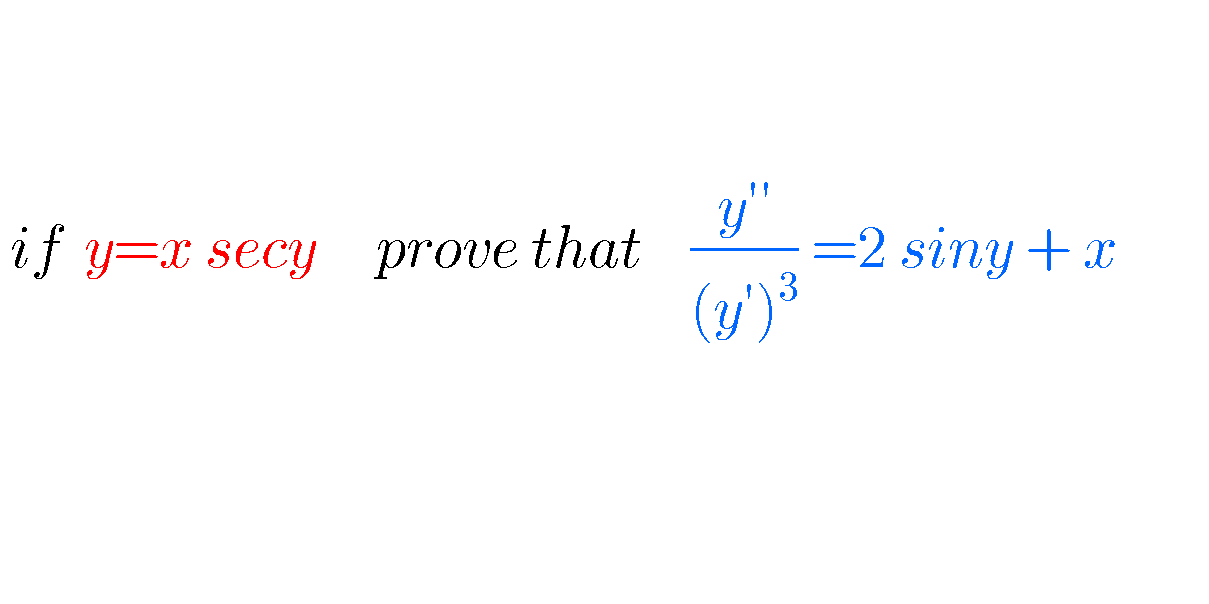
Answered by $@ty@m123 last updated on 14/Dec/19
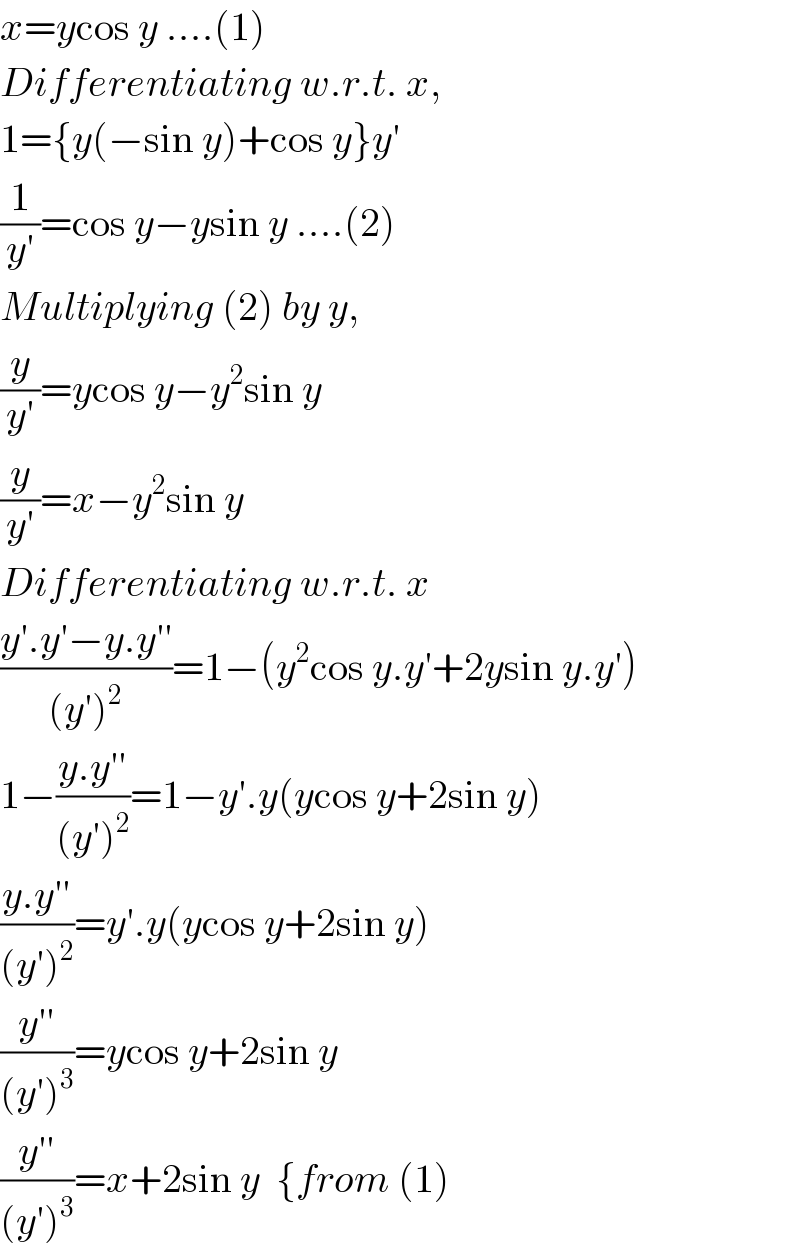
$${x}={y}\mathrm{cos}\:{y}\:….\left(\mathrm{1}\right) \\ $$$${Differentiating}\:{w}.{r}.{t}.\:{x}, \\ $$$$\mathrm{1}=\left\{{y}\left(−\mathrm{sin}\:{y}\right)+\mathrm{cos}\:{y}\right\}{y}' \\ $$$$\frac{\mathrm{1}}{{y}'}=\mathrm{cos}\:{y}−{y}\mathrm{sin}\:{y}\:….\left(\mathrm{2}\right) \\ $$$${Multiplying}\:\left(\mathrm{2}\right)\:{by}\:{y}, \\ $$$$\frac{{y}}{{y}'}={y}\mathrm{cos}\:{y}−{y}^{\mathrm{2}} \mathrm{sin}\:{y} \\ $$$$\frac{{y}}{{y}'}={x}−{y}^{\mathrm{2}} \mathrm{sin}\:{y} \\ $$$${Differentiating}\:{w}.{r}.{t}.\:{x} \\ $$$$\frac{{y}'.{y}'−{y}.{y}''}{\left({y}'\right)^{\mathrm{2}} }=\mathrm{1}−\left({y}^{\mathrm{2}} \mathrm{cos}\:{y}.{y}'+\mathrm{2}{y}\mathrm{sin}\:{y}.{y}'\right) \\ $$$$\mathrm{1}−\frac{{y}.{y}''}{\left({y}'\right)^{\mathrm{2}} }=\mathrm{1}−{y}'.{y}\left({y}\mathrm{cos}\:{y}+\mathrm{2sin}\:{y}\right) \\ $$$$\frac{{y}.{y}''}{\left({y}'\right)^{\mathrm{2}} }={y}'.{y}\left({y}\mathrm{cos}\:{y}+\mathrm{2sin}\:{y}\right) \\ $$$$\frac{{y}''}{\left({y}'\right)^{\mathrm{3}} }={y}\mathrm{cos}\:{y}+\mathrm{2sin}\:{y} \\ $$$$\frac{{y}''}{\left({y}'\right)^{\mathrm{3}} }={x}+\mathrm{2sin}\:{y}\:\:\left\{{from}\:\left(\mathrm{1}\right)\right. \\ $$
