Question Number 131885 by Study last updated on 09/Feb/21
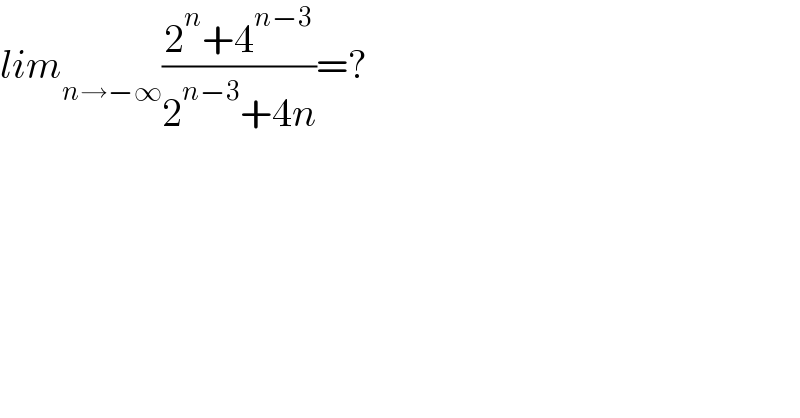
$${lim}_{{n}\rightarrow−\infty} \frac{\mathrm{2}^{{n}} +\mathrm{4}^{{n}−\mathrm{3}} }{\mathrm{2}^{{n}−\mathrm{3}} +\mathrm{4}{n}}=? \\ $$
Commented by malwan last updated on 09/Feb/21
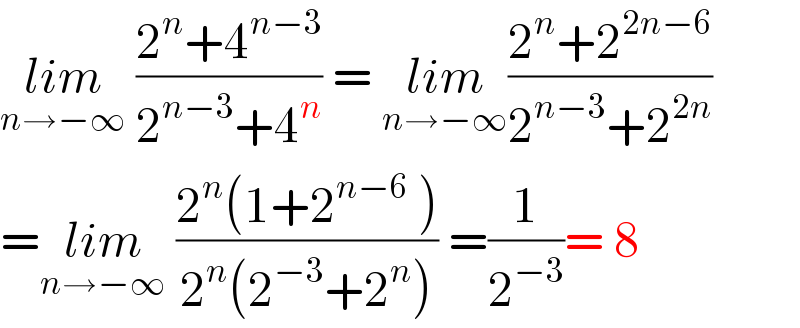
$$\underset{{n}\rightarrow−\infty} {{lim}}\:\frac{\mathrm{2}^{{n}} +\mathrm{4}^{{n}−\mathrm{3}} }{\mathrm{2}^{{n}−\mathrm{3}} +\mathrm{4}^{{n}} }\:=\:\underset{{n}\rightarrow−\infty} {{lim}}\frac{\mathrm{2}^{{n}} +\mathrm{2}^{\mathrm{2}{n}−\mathrm{6}} }{\mathrm{2}^{{n}−\mathrm{3}} +\mathrm{2}^{\mathrm{2}{n}} } \\ $$$$=\underset{{n}\rightarrow−\infty} {{lim}}\:\frac{\mathrm{2}^{{n}} \left(\mathrm{1}+\mathrm{2}^{{n}−\mathrm{6}} \:\right)}{\mathrm{2}^{{n}} \left(\mathrm{2}^{−\mathrm{3}} +\mathrm{2}^{{n}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}^{−\mathrm{3}} }=\:\mathrm{8} \\ $$
Answered by EDWIN88 last updated on 10/Feb/21
![if lim_(n→−∞) (((2^n +4^(n−3) )/(2^(n−3) +4^n )))=lim_(n→−∞) (((4^n [((2/4))^n +(1/(64)) ])/(4^n [1+(1/8)((2/4))^n )) ) = lim_(n→−∞) ((((1/2^n )+(1/(64)))/(1+(1/8).(1/2^n ))))=lim_(n→−∞) (((1+64.2^n )/(2^n +(1/8))))= 8 note that lim_(n→−∞) 2^n = 0](https://www.tinkutara.com/question/Q131958.png)
$$\mathrm{if}\:\underset{\mathrm{n}\rightarrow−\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}^{\mathrm{n}} +\mathrm{4}^{\mathrm{n}−\mathrm{3}} }{\mathrm{2}^{\mathrm{n}−\mathrm{3}} +\mathrm{4}^{\mathrm{n}} }\right)=\underset{\mathrm{n}\rightarrow−\infty} {\mathrm{lim}}\left(\frac{\mathrm{4}^{\mathrm{n}} \left[\left(\frac{\mathrm{2}}{\mathrm{4}}\right)^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{64}}\:\right]}{\mathrm{4}^{\mathrm{n}} \left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{2}}{\mathrm{4}}\right)^{\mathrm{n}} \right.}\:\right) \\ $$$$=\:\underset{\mathrm{n}\rightarrow−\infty} {\mathrm{lim}}\left(\frac{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }+\frac{\mathrm{1}}{\mathrm{64}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{8}}.\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }}\right)=\underset{\mathrm{n}\rightarrow−\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}+\mathrm{64}.\mathrm{2}^{\mathrm{n}} }{\mathrm{2}^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{8}}}\right)=\:\mathrm{8} \\ $$$$\mathrm{note}\:\mathrm{that}\:\underset{\mathrm{n}\rightarrow−\infty} {\mathrm{lim}2}^{\mathrm{n}} \:=\:\mathrm{0}\: \\ $$
Answered by liberty last updated on 10/Feb/21
![If lim_(n→−∞) (((2^n +4^(n−3) )/(2^(n−3) +4^n ))) let 2^n = x where x→0, as n→−∞ then lim_(x→0) ((x+(1/(64))x^2 )/((1/8)x+x^2 )) = lim_(x→0) ((64x+x^2 )/(8x+64x^2 )) = lim_(x→0) [ ((64+x)/(8+64x))] = ((64)/8)=8](https://www.tinkutara.com/question/Q131959.png)
$$\mathrm{If}\:\underset{\mathrm{n}\rightarrow−\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}^{\mathrm{n}} +\mathrm{4}^{\mathrm{n}−\mathrm{3}} }{\mathrm{2}^{\mathrm{n}−\mathrm{3}} +\mathrm{4}^{\mathrm{n}} }\right) \\ $$$$\:\mathrm{let}\:\mathrm{2}^{\mathrm{n}} =\:\mathrm{x}\:\mathrm{where}\:\mathrm{x}\rightarrow\mathrm{0},\:\mathrm{as}\:\mathrm{n}\rightarrow−\infty \\ $$$$\mathrm{then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{64}}\mathrm{x}^{\mathrm{2}} }{\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}+\mathrm{x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{64x}+\mathrm{x}^{\mathrm{2}} }{\mathrm{8x}+\mathrm{64x}^{\mathrm{2}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\:\frac{\mathrm{64}+\mathrm{x}}{\mathrm{8}+\mathrm{64x}}\right]\:=\:\frac{\mathrm{64}}{\mathrm{8}}=\mathrm{8} \\ $$
