sin-ln-x-dx-Please-

Question Number 141336 by cesarL last updated on 17/May/21

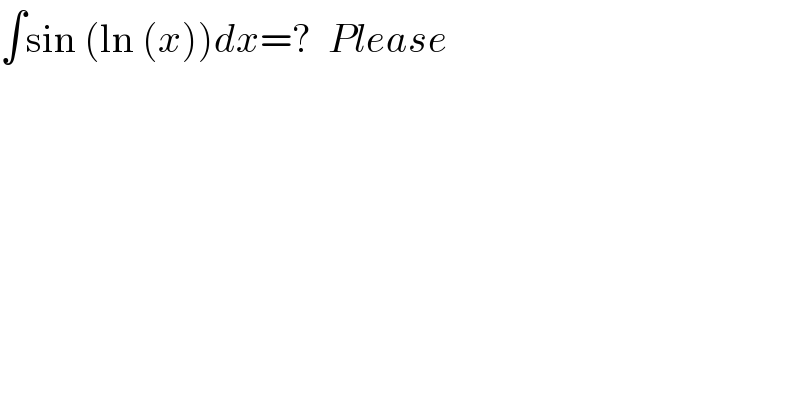
$$\int\mathrm{sin}\:\left(\mathrm{ln}\:\left({x}\right)\right){dx}=?\:\:{Please} \\ $$

Answered by Dwaipayan Shikari last updated on 17/May/21

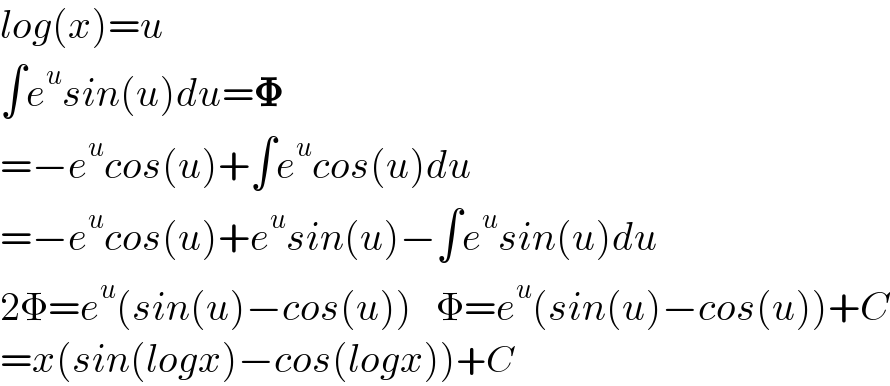
log(x)=u ∫e^u sin(u)du=𝚽 =−e^u cos(u)+∫e^u cos(u)du =−e^u cos(u)+e^u sin(u)−∫e^u sin(u)du 2Φ=e^u (sin(u)−cos(u)) Φ=e^u (sin(u)−cos(u))+C =x(sin(logx)−cos(logx))+C

$${log}\left({x}\right)={u} \\ $$$$\int{e}^{{u}} {sin}\left({u}\right){du}=\boldsymbol{\Phi} \\ $$$$=−{e}^{{u}} {cos}\left({u}\right)+\int{e}^{{u}} {cos}\left({u}\right){du} \\ $$$$=−{e}^{{u}} {cos}\left({u}\right)+{e}^{{u}} {sin}\left({u}\right)−\int{e}^{{u}} {sin}\left({u}\right){du} \\ $$$$\mathrm{2}\Phi={e}^{{u}} \left({sin}\left({u}\right)−{cos}\left({u}\right)\right)\:\:\:\Phi={e}^{{u}} \left({sin}\left({u}\right)−{cos}\left({u}\right)\right)+{C} \\ $$$$={x}\left({sin}\left({logx}\right)−{cos}\left({logx}\right)\right)+{C} \\ $$

Answered by qaz last updated on 17/May/21

∫x^(n−1) dx=(x^n /n)+C n=1+i x^i =e^(ilnx) =cos (lnx)+isin (lnx) (x^n /n)=((1−i)/2)[cos (lnx)+isin (lnx)]x ⇒∫sin (lnx)dx=(x/2)[sin (lnx)−cos (lnx)]+C −−−−−−−−−−−−−−−−− y=lnx x=e^y ∫sin (lnx)dx=∫e^y sin ydy =(1/D)e^y sin y=e^y (1/(D+1))sin y=e^y ((1−D)/(1−D^2 ))sin y =e^y ((1−D)/(1−i^2 ))sin y=(e^y /2)(sin y−cos y) =(x/2)[sin (lnx)−cos (lnx)]+C

$$\int{x}^{{n}−\mathrm{1}} {dx}=\frac{{x}^{{n}} }{{n}}+{C} \\ $$$${n}=\mathrm{1}+{i} \\ $$$${x}^{{i}} ={e}^{{ilnx}} =\mathrm{cos}\:\left({lnx}\right)+{i}\mathrm{sin}\:\left({lnx}\right) \\ $$$$\frac{{x}^{{n}} }{{n}}=\frac{\mathrm{1}−{i}}{\mathrm{2}}\left[\mathrm{cos}\:\left({lnx}\right)+{i}\mathrm{sin}\:\left({lnx}\right)\right]{x} \\ $$$$\Rightarrow\int\mathrm{sin}\:\left({lnx}\right){dx}=\frac{{x}}{\mathrm{2}}\left[\mathrm{sin}\:\left({lnx}\right)−\mathrm{cos}\:\left({lnx}\right)\right]+{C} \\ $$$$−−−−−−−−−−−−−−−−− \\ $$$${y}={lnx} \\ $$$${x}={e}^{{y}} \\ $$$$\int\mathrm{sin}\:\left({lnx}\right){dx}=\int{e}^{{y}} \mathrm{sin}\:{ydy} \\ $$$$=\frac{\mathrm{1}}{{D}}{e}^{{y}} \mathrm{sin}\:{y}={e}^{{y}} \frac{\mathrm{1}}{{D}+\mathrm{1}}\mathrm{sin}\:{y}={e}^{{y}} \frac{\mathrm{1}−{D}}{\mathrm{1}−{D}^{\mathrm{2}} }\mathrm{sin}\:{y} \\ $$$$={e}^{{y}} \frac{\mathrm{1}−{D}}{\mathrm{1}−{i}^{\mathrm{2}} }\mathrm{sin}\:{y}=\frac{{e}^{{y}} }{\mathrm{2}}\left(\mathrm{sin}\:{y}−\mathrm{cos}\:{y}\right) \\ $$$$=\frac{{x}}{\mathrm{2}}\left[\mathrm{sin}\:\left({lnx}\right)−\mathrm{cos}\:\left({lnx}\right)\right]+{C} \\ $$

Commented by cesarL last updated on 17/May/21

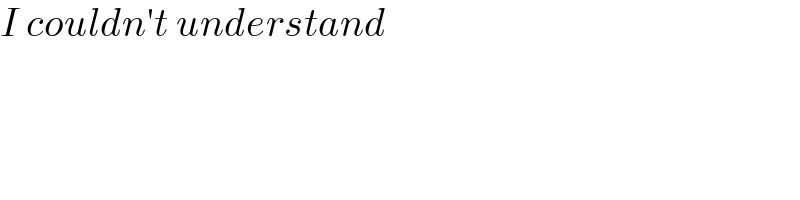
$${I}\:{couldn}'{t}\:{understand} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply