Question Number 75814 by Master last updated on 18/Dec/19
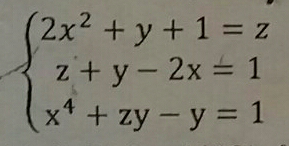
Commented by Master last updated on 18/Dec/19

$$\mathrm{xyz}=? \\ $$
Answered by mr W last updated on 18/Dec/19
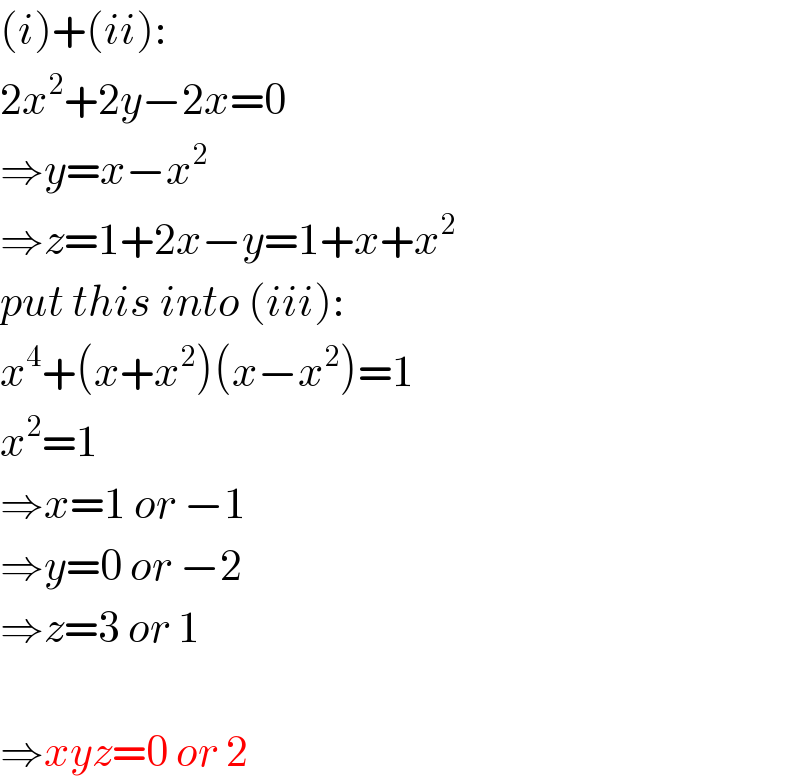
$$\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}−\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow{y}={x}−{x}^{\mathrm{2}} \\ $$$$\Rightarrow{z}=\mathrm{1}+\mathrm{2}{x}−{y}=\mathrm{1}+{x}+{x}^{\mathrm{2}} \\ $$$${put}\:{this}\:{into}\:\left({iii}\right): \\ $$$${x}^{\mathrm{4}} +\left({x}+{x}^{\mathrm{2}} \right)\left({x}−{x}^{\mathrm{2}} \right)=\mathrm{1} \\ $$$${x}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{1}\:{or}\:−\mathrm{1} \\ $$$$\Rightarrow{y}=\mathrm{0}\:{or}\:−\mathrm{2} \\ $$$$\Rightarrow{z}=\mathrm{3}\:{or}\:\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow{xyz}=\mathrm{0}\:{or}\:\mathrm{2} \\ $$
