Question Number 10294 by Tawakalitu ayo mi last updated on 02/Feb/17

$$\mathrm{A}\:\mathrm{student}\:\mathrm{needs}\:\mathrm{at}\:\mathrm{least}\:\mathrm{three}\:\mathrm{notebooks}\:\mathrm{and} \\ $$$$\mathrm{three}\:\mathrm{pencils}.\:\mathrm{Notebooks}\:\mathrm{cost}\:#\mathrm{60}\:\mathrm{and}\:\mathrm{pencil} \\ $$$$#\mathrm{36}\:\mathrm{and}\:\mathrm{the}\:\mathrm{student}\:\mathrm{has}\:#\mathrm{360}\:\mathrm{to}\:\mathrm{spend}.\:\mathrm{The} \\ $$$$\mathrm{student}\:\mathrm{decides}\:\mathrm{to}\:\mathrm{spend}\:\mathrm{as}\:\mathrm{much}\:\mathrm{as}\:\mathrm{possible} \\ $$$$\mathrm{of}\:\mathrm{his}\:#\mathrm{360}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{he}\:\mathrm{spend}\:\mathrm{his}\:\mathrm{money} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Does}\:\mathrm{any}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ways}\:\mathrm{give}\:\mathrm{him}\:\mathrm{change}\:??? \\ $$$$\mathrm{if}\:\mathrm{so},\:\mathrm{how}\:\mathrm{much}\:? \\ $$
Answered by mrW1 last updated on 02/Feb/17

$${for}\:\mathrm{3}\:{notebooks}\:{and}\:\mathrm{3}\:{pencils}: \\ $$$$\mathrm{3}×\mathrm{60}+\mathrm{3}×\mathrm{36}=\mathrm{288} \\ $$$$ \\ $$$${money}\:{left}: \\ $$$$\mathrm{360}−\mathrm{288}=\mathrm{72} \\ $$$$ \\ $$$${there}\:{are}\:\mathrm{2}\:{ways}\:{to}\:{spend}\:{this}\:{money}: \\ $$$${way}\:\mathrm{1}:\:{to}\:{buy}\:\mathrm{2}\:{additional}\:{pencils}\:{for}\:\mathrm{2}×\mathrm{36}=#\mathrm{72} \\ $$$${way}\:\mathrm{2}:\:{to}\:{buy}\:\mathrm{1}\:{additional}\:{notebook}\:{for}\:#\mathrm{60}. \\ $$$$ \\ $$$${way}\:\mathrm{2}\:{gives}\:{ihm}\:{a}\:{change}\:{of}\:#\mathrm{12}. \\ $$
Commented by Tawakalitu ayo mi last updated on 02/Feb/17

$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by sandy_suhendra last updated on 02/Feb/17
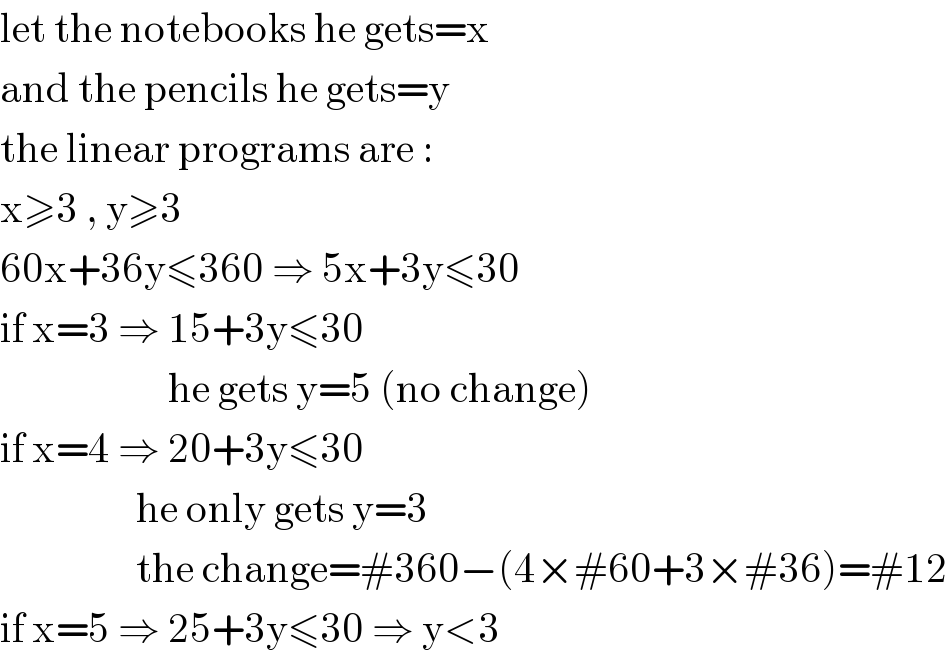
$$\mathrm{let}\:\mathrm{the}\:\mathrm{notebooks}\:\mathrm{he}\:\mathrm{gets}=\mathrm{x} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{pencils}\:\mathrm{he}\:\mathrm{gets}=\mathrm{y} \\ $$$$\mathrm{the}\:\mathrm{linear}\:\mathrm{programs}\:\mathrm{are}\:: \\ $$$$\mathrm{x}\geqslant\mathrm{3}\:,\:\mathrm{y}\geqslant\mathrm{3} \\ $$$$\mathrm{60x}+\mathrm{36y}\leqslant\mathrm{360}\:\Rightarrow\:\mathrm{5x}+\mathrm{3y}\leqslant\mathrm{30} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{3}\:\Rightarrow\:\mathrm{15}+\mathrm{3y}\leqslant\mathrm{30} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{he}\:\mathrm{gets}\:\mathrm{y}=\mathrm{5}\:\left(\mathrm{no}\:\mathrm{change}\right) \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{4}\:\Rightarrow\:\mathrm{20}+\mathrm{3y}\leqslant\mathrm{30} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{he}\:\mathrm{only}\:\mathrm{gets}\:\mathrm{y}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{the}\:\mathrm{change}=#\mathrm{360}−\left(\mathrm{4}×#\mathrm{60}+\mathrm{3}×#\mathrm{36}\right)=#\mathrm{12} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{5}\:\Rightarrow\:\mathrm{25}+\mathrm{3y}\leqslant\mathrm{30}\:\Rightarrow\:\mathrm{y}<\mathrm{3} \\ $$
Commented by Tawakalitu ayo mi last updated on 02/Feb/17

$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by arge last updated on 03/Feb/17
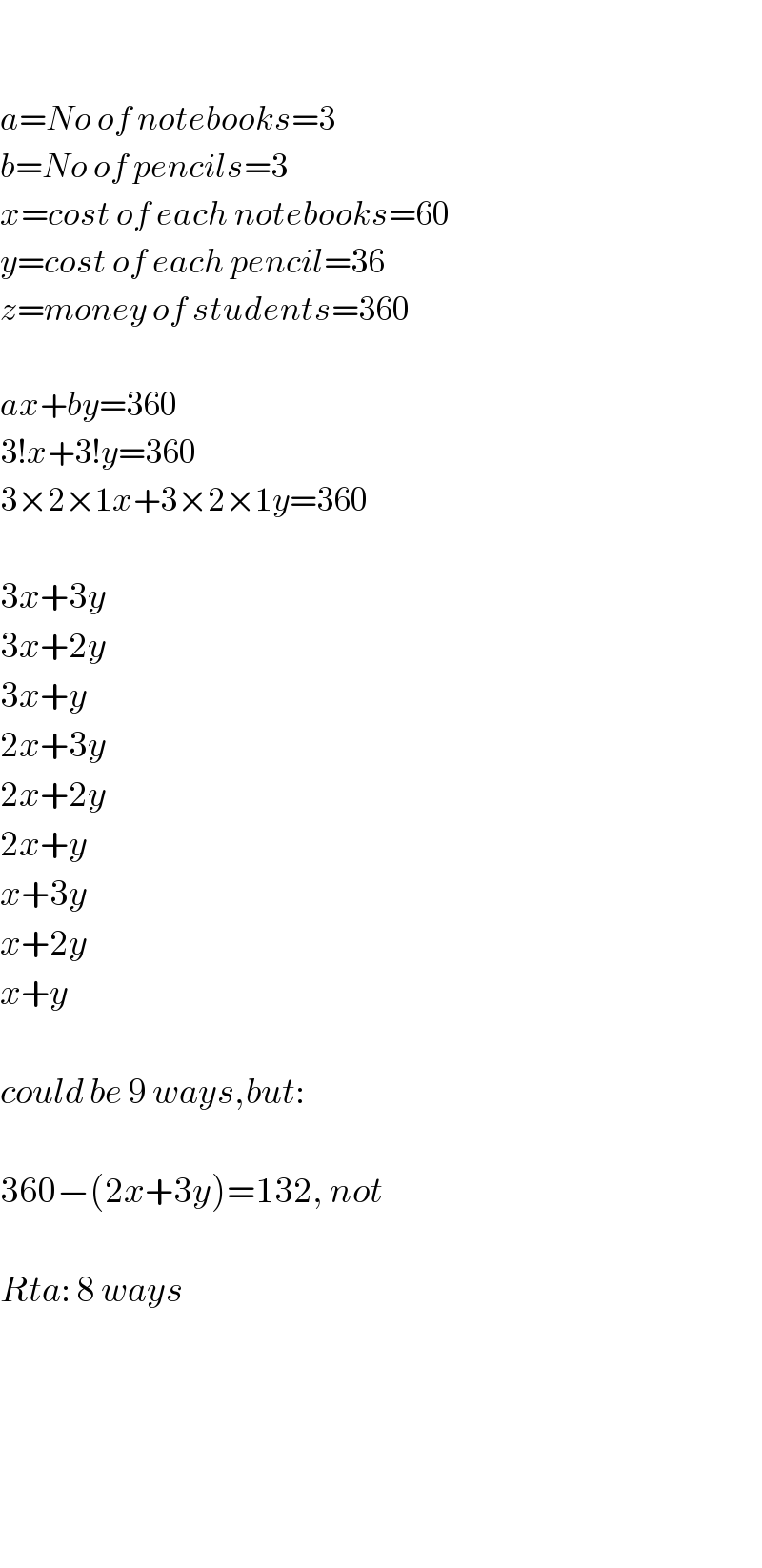
$$ \\ $$$$ \\ $$$${a}={No}\:{of}\:{notebooks}=\mathrm{3} \\ $$$${b}={No}\:{of}\:{pencils}=\mathrm{3} \\ $$$${x}={cost}\:{of}\:{each}\:{notebooks}=\mathrm{60} \\ $$$${y}={cost}\:{of}\:{each}\:{pencil}=\mathrm{36} \\ $$$${z}={money}\:{of}\:{students}=\mathrm{360} \\ $$$$ \\ $$$${ax}+{by}=\mathrm{360} \\ $$$$\mathrm{3}!{x}+\mathrm{3}!{y}=\mathrm{360} \\ $$$$\mathrm{3}×\mathrm{2}×\mathrm{1}{x}+\mathrm{3}×\mathrm{2}×\mathrm{1}{y}=\mathrm{360} \\ $$$$ \\ $$$$\mathrm{3}{x}+\mathrm{3}{y} \\ $$$$\mathrm{3}{x}+\mathrm{2}{y} \\ $$$$\mathrm{3}{x}+{y} \\ $$$$\mathrm{2}{x}+\mathrm{3}{y} \\ $$$$\mathrm{2}{x}+\mathrm{2}{y} \\ $$$$\mathrm{2}{x}+{y} \\ $$$${x}+\mathrm{3}{y} \\ $$$${x}+\mathrm{2}{y} \\ $$$${x}+{y} \\ $$$$ \\ $$$${could}\:{be}\:\mathrm{9}\:{ways},{but}: \\ $$$$ \\ $$$$\mathrm{360}−\left(\mathrm{2}{x}+\mathrm{3}{y}\right)=\mathrm{132},\:{not} \\ $$$$ \\ $$$${Rta}:\:\mathrm{8}\:{ways} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawakalitu ayo mi last updated on 03/Feb/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
