Question Number 141372 by iloveisrael last updated on 18/May/21

Answered by EDWIN88 last updated on 18/May/21
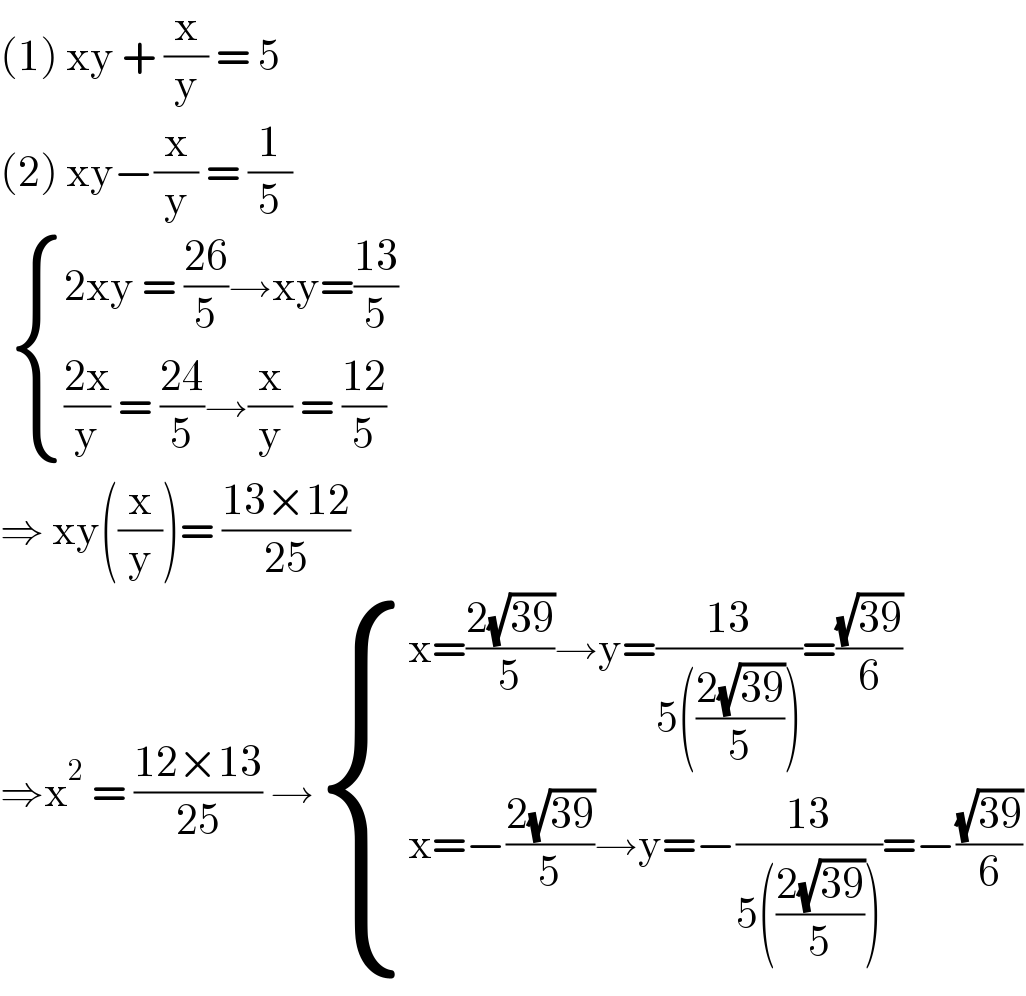
$$\left(\mathrm{1}\right)\:\mathrm{xy}\:+\:\frac{\mathrm{x}}{\mathrm{y}}\:=\:\mathrm{5} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{xy}−\frac{\mathrm{x}}{\mathrm{y}}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\:\begin{cases}{\mathrm{2xy}\:=\:\frac{\mathrm{26}}{\mathrm{5}}\rightarrow\mathrm{xy}=\frac{\mathrm{13}}{\mathrm{5}}}\\{\frac{\mathrm{2x}}{\mathrm{y}}\:=\:\frac{\mathrm{24}}{\mathrm{5}}\rightarrow\frac{\mathrm{x}}{\mathrm{y}}\:=\:\frac{\mathrm{12}}{\mathrm{5}}}\end{cases} \\ $$$$\Rightarrow\:\mathrm{xy}\left(\frac{\mathrm{x}}{\mathrm{y}}\right)=\:\frac{\mathrm{13}×\mathrm{12}}{\mathrm{25}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \:=\:\frac{\mathrm{12}×\mathrm{13}}{\mathrm{25}}\:\rightarrow\begin{cases}{\mathrm{x}=\frac{\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{5}}\rightarrow\mathrm{y}=\frac{\mathrm{13}}{\mathrm{5}\left(\frac{\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{5}}\right)}=\frac{\sqrt{\mathrm{39}}}{\mathrm{6}}}\\{\mathrm{x}=−\frac{\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{5}}\rightarrow\mathrm{y}=−\frac{\mathrm{13}}{\mathrm{5}\left(\frac{\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{5}}\right)}=−\frac{\sqrt{\mathrm{39}}}{\mathrm{6}}}\end{cases} \\ $$
Answered by MJS_new last updated on 18/May/21
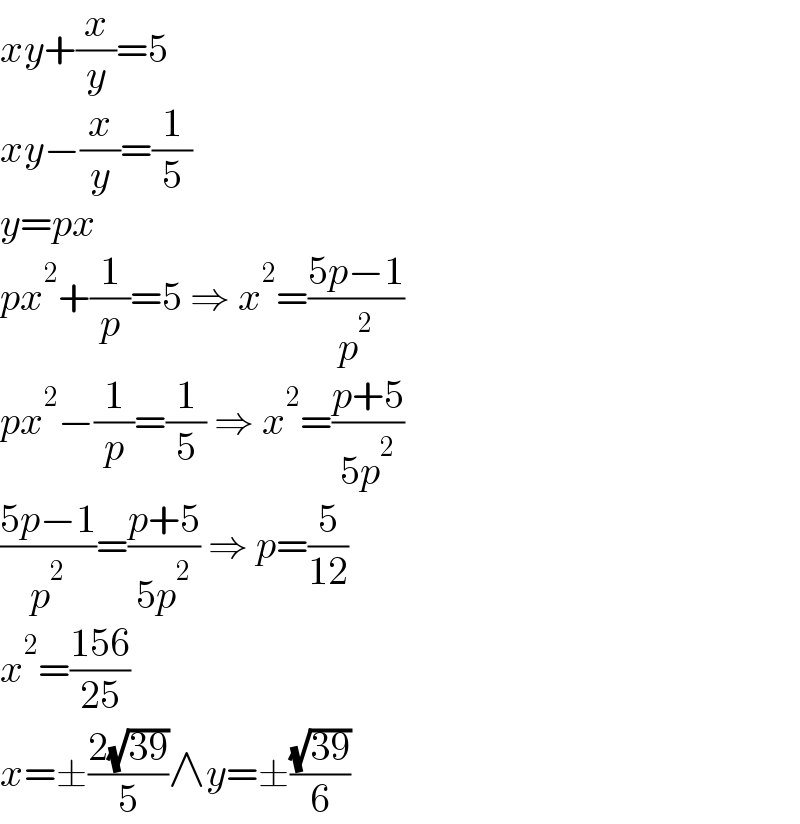
$${xy}+\frac{{x}}{{y}}=\mathrm{5} \\ $$$${xy}−\frac{{x}}{{y}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${y}={px} \\ $$$${px}^{\mathrm{2}} +\frac{\mathrm{1}}{{p}}=\mathrm{5}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{5}{p}−\mathrm{1}}{{p}^{\mathrm{2}} } \\ $$$${px}^{\mathrm{2}} −\frac{\mathrm{1}}{{p}}=\frac{\mathrm{1}}{\mathrm{5}}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{{p}+\mathrm{5}}{\mathrm{5}{p}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{5}{p}−\mathrm{1}}{{p}^{\mathrm{2}} }=\frac{{p}+\mathrm{5}}{\mathrm{5}{p}^{\mathrm{2}} }\:\Rightarrow\:{p}=\frac{\mathrm{5}}{\mathrm{12}} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{156}}{\mathrm{25}} \\ $$$${x}=\pm\frac{\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{5}}\wedge{y}=\pm\frac{\sqrt{\mathrm{39}}}{\mathrm{6}} \\ $$
Answered by Rasheed.Sindhi last updated on 18/May/21
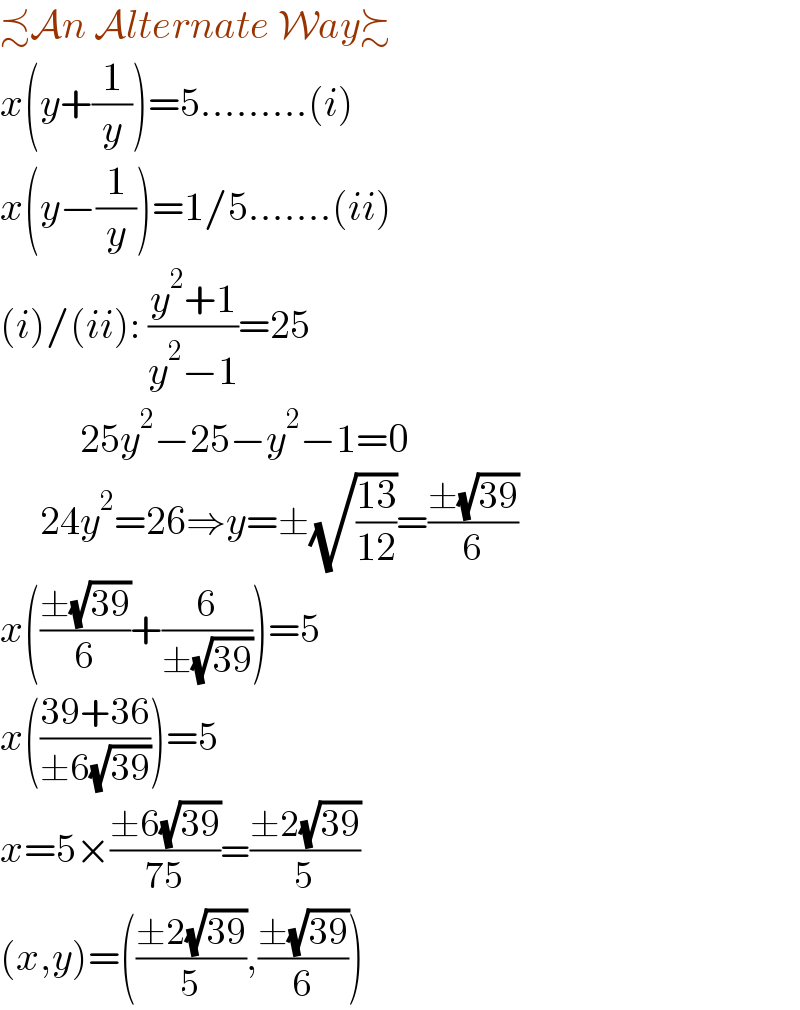
$$\precsim\mathcal{A}{n}\:\mathcal{A}{lternate}\:\mathcal{W}{ay}\succsim \\ $$$${x}\left({y}+\frac{\mathrm{1}}{{y}}\right)=\mathrm{5}………\left({i}\right) \\ $$$${x}\left({y}−\frac{\mathrm{1}}{{y}}\right)=\mathrm{1}/\mathrm{5}…….\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right):\:\frac{{y}^{\mathrm{2}} +\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{1}}=\mathrm{25} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{25}{y}^{\mathrm{2}} −\mathrm{25}−{y}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{24}{y}^{\mathrm{2}} =\mathrm{26}\Rightarrow{y}=\pm\sqrt{\frac{\mathrm{13}}{\mathrm{12}}}=\frac{\pm\sqrt{\mathrm{39}}}{\mathrm{6}} \\ $$$${x}\left(\frac{\pm\sqrt{\mathrm{39}}}{\mathrm{6}}+\frac{\mathrm{6}}{\pm\sqrt{\mathrm{39}}}\right)=\mathrm{5} \\ $$$${x}\left(\frac{\mathrm{39}+\mathrm{36}}{\pm\mathrm{6}\sqrt{\mathrm{39}}}\right)=\mathrm{5} \\ $$$${x}=\mathrm{5}×\frac{\pm\mathrm{6}\sqrt{\mathrm{39}}}{\mathrm{75}}=\frac{\pm\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{5}} \\ $$$$\left({x},{y}\right)=\left(\frac{\pm\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{5}},\frac{\pm\sqrt{\mathrm{39}}}{\mathrm{6}}\right) \\ $$
