Question Number 66379 by Sandy Suhendra last updated on 13/Aug/19
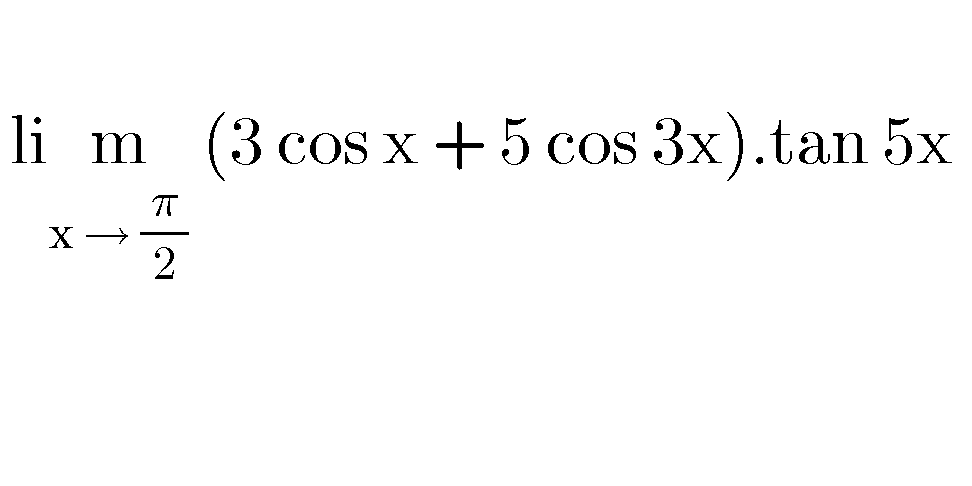
Commented by kaivan.ahmadi last updated on 13/Aug/19
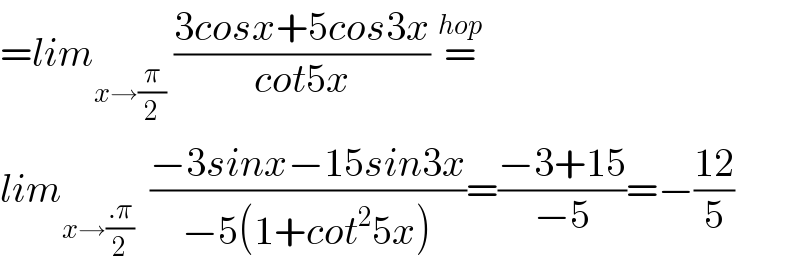
$$={lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{3}{cosx}+\mathrm{5}{cos}\mathrm{3}{x}}{{cot}\mathrm{5}{x}}\:\overset{{hop}} {=} \\ $$$${lim}_{{x}\rightarrow\frac{.\pi}{\mathrm{2}}} \:\:\frac{−\mathrm{3}{sinx}−\mathrm{15}{sin}\mathrm{3}{x}}{−\mathrm{5}\left(\mathrm{1}+{cot}^{\mathrm{2}} \mathrm{5}{x}\right)}=\frac{−\mathrm{3}+\mathrm{15}}{−\mathrm{5}}=−\frac{\mathrm{12}}{\mathrm{5}} \\ $$
Commented by mathmax by abdo last updated on 14/Aug/19
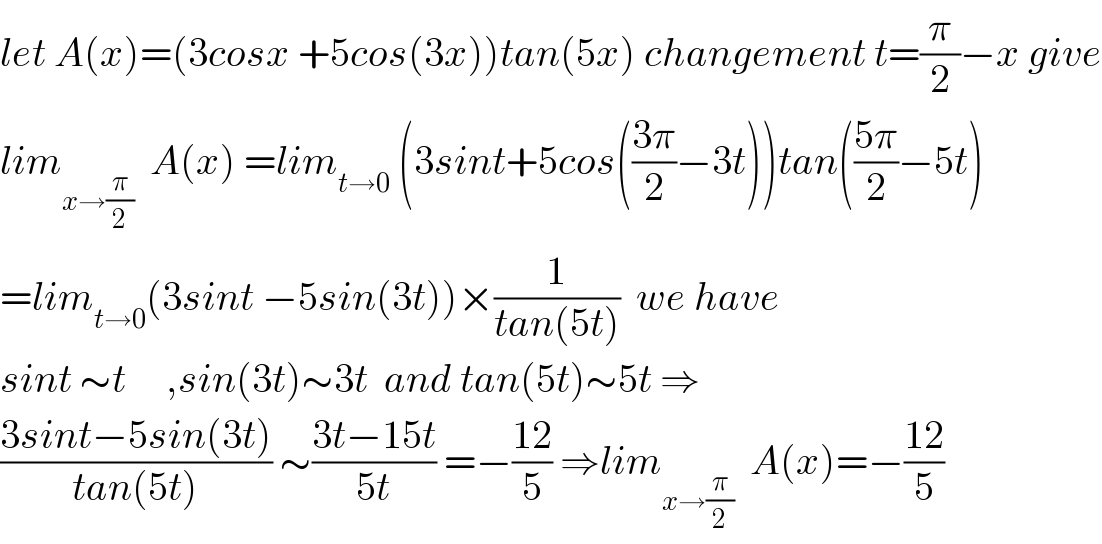
$${let}\:{A}\left({x}\right)=\left(\mathrm{3}{cosx}\:+\mathrm{5}{cos}\left(\mathrm{3}{x}\right)\right){tan}\left(\mathrm{5}{x}\right)\:{changement}\:{t}=\frac{\pi}{\mathrm{2}}−{x}\:{give} \\ $$$${lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:{A}\left({x}\right)\:={lim}_{{t}\rightarrow\mathrm{0}} \:\left(\mathrm{3}{sint}+\mathrm{5}{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}−\mathrm{3}{t}\right)\right){tan}\left(\frac{\mathrm{5}\pi}{\mathrm{2}}−\mathrm{5}{t}\right) \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \left(\mathrm{3}{sint}\:−\mathrm{5}{sin}\left(\mathrm{3}{t}\right)\right)×\frac{\mathrm{1}}{{tan}\left(\mathrm{5}{t}\right)}\:\:{we}\:{have}\: \\ $$$${sint}\:\sim{t}\:\:\:\:\:,{sin}\left(\mathrm{3}{t}\right)\sim\mathrm{3}{t}\:\:{and}\:{tan}\left(\mathrm{5}{t}\right)\sim\mathrm{5}{t}\:\Rightarrow \\ $$$$\frac{\mathrm{3}{sint}−\mathrm{5}{sin}\left(\mathrm{3}{t}\right)}{{tan}\left(\mathrm{5}{t}\right)}\:\sim\frac{\mathrm{3}{t}−\mathrm{15}{t}}{\mathrm{5}{t}}\:=−\frac{\mathrm{12}}{\mathrm{5}}\:\Rightarrow{lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:{A}\left({x}\right)=−\frac{\mathrm{12}}{\mathrm{5}} \\ $$
