Question Number 10364 by Joel575 last updated on 05/Feb/17
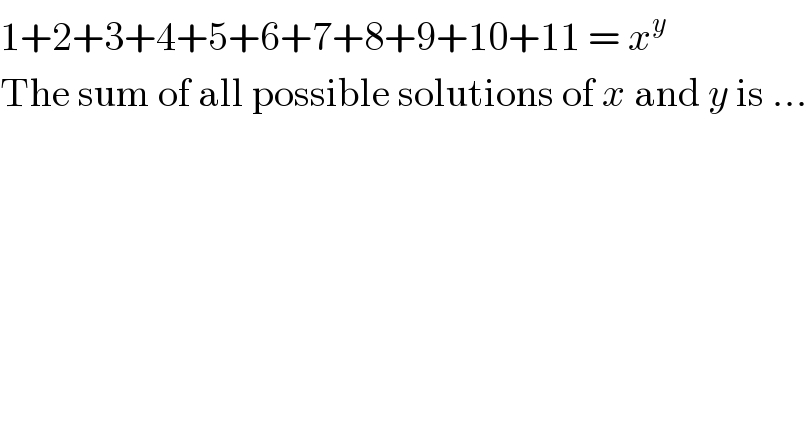
$$\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}+\mathrm{9}+\mathrm{10}+\mathrm{11}\:=\:{x}^{{y}} \\ $$$$\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{solutions}\:\mathrm{of}\:{x}\:\mathrm{and}\:{y}\:\mathrm{is}\:… \\ $$
Answered by mrW1 last updated on 05/Feb/17

$$\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}+\mathrm{9}+\mathrm{10}+\mathrm{11}=\frac{\mathrm{11}×\mathrm{12}}{\mathrm{2}}=\mathrm{66} \\ $$$${x}^{{y}} =\mathrm{66} \\ $$$${y}\mathrm{ln}\:{x}=\mathrm{ln}\:\mathrm{66} \\ $$$${y}=\frac{\mathrm{ln}\:\mathrm{66}}{\mathrm{ln}\:{x}} \\ $$$${x}\in{R},{x}>\mathrm{0},\:{x}\neq\mathrm{1} \\ $$$$\Rightarrow{if}\:{x}\:{and}\:{y}\:{can}\:{be}\:{real}\:{numbers}, \\ $$$${there}\:{are}\:{infinite}\:{solutions}. \\ $$$$ \\ $$$${if}\:{x}\:{and}\:{y}\:{are}\:{integers},\:{there}\:{is}\:{only} \\ $$$${one}\:{solution}: \\ $$$${x}=\mathrm{66},\:{y}=\mathrm{1} \\ $$$${since}\:\mathrm{66}=\mathrm{2}×\mathrm{3}×\mathrm{11} \\ $$
Commented by Joel575 last updated on 06/Feb/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sirr} \\ $$$$ \\ $$
