Question Number 75939 by ahmadshahhimat775@gmail.com last updated on 21/Dec/19

Commented by JDamian last updated on 21/Dec/19

$$\left.{c}\right)\:\left({n}!\right)^{\frac{\mathrm{1}}{{n}}} \\ $$
Commented by mathmax by abdo last updated on 21/Dec/19
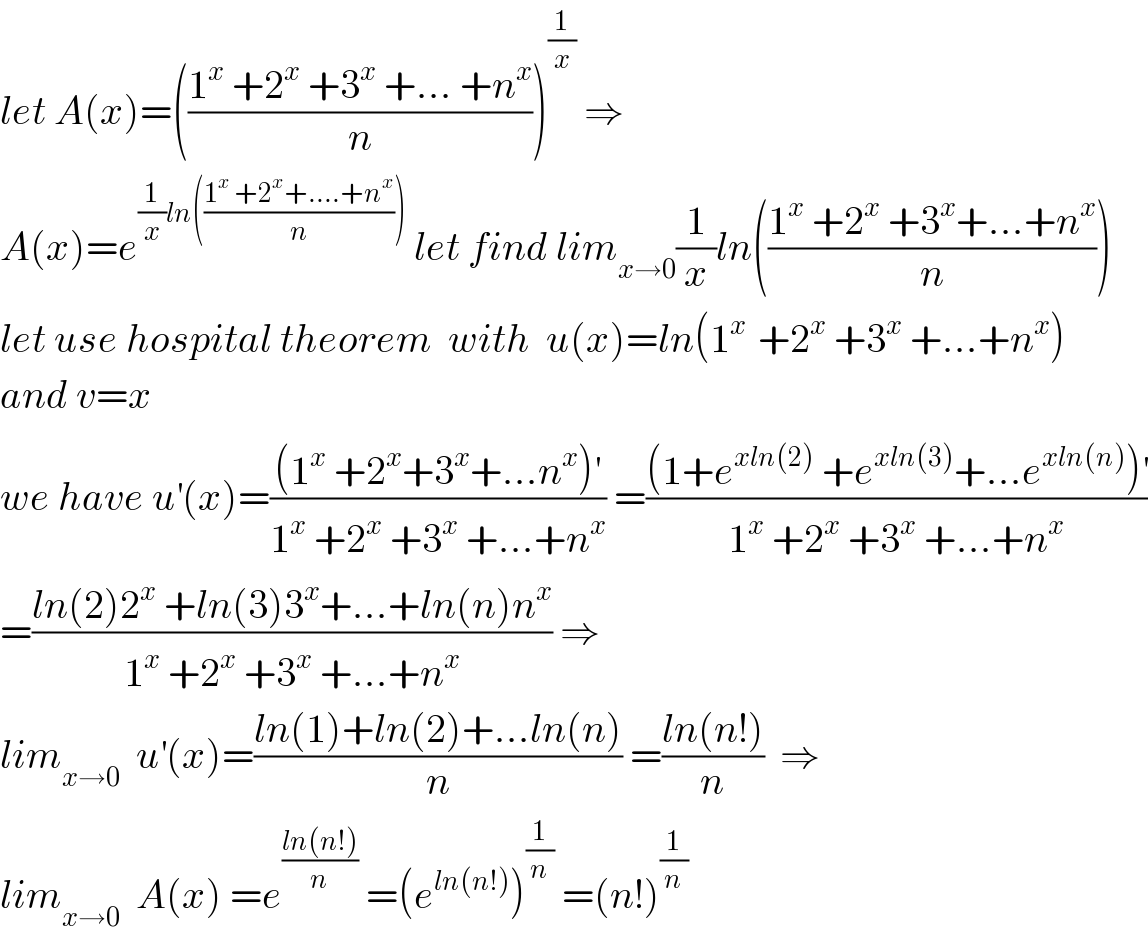
$${let}\:{A}\left({x}\right)=\left(\frac{\mathrm{1}^{{x}} \:+\mathrm{2}^{{x}} \:+\mathrm{3}^{{x}} \:+…\:+{n}^{{x}} }{{n}}\right)^{\frac{\mathrm{1}}{{x}}} \:\Rightarrow \\ $$$${A}\left({x}\right)={e}^{\frac{\mathrm{1}}{{x}}{ln}\left(\frac{\mathrm{1}^{{x}} \:+\mathrm{2}^{{x}} +….+{n}^{{x}} }{{n}}\right)} \:{let}\:{find}\:{lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}}{{x}}{ln}\left(\frac{\mathrm{1}^{{x}} \:+\mathrm{2}^{{x}} \:+\mathrm{3}^{{x}} +…+{n}^{{x}} }{{n}}\right) \\ $$$${let}\:{use}\:{hospital}\:{theorem}\:\:{with}\:\:{u}\left({x}\right)={ln}\left(\mathrm{1}^{{x}\:} \:+\mathrm{2}^{{x}} \:+\mathrm{3}^{{x}} \:+…+{n}^{{x}} \right) \\ $$$${and}\:{v}={x} \\ $$$${we}\:{have}\:{u}^{'} \left({x}\right)=\frac{\left(\mathrm{1}^{{x}} \:+\mathrm{2}^{{x}} +\mathrm{3}^{{x}} +…{n}^{{x}} \right)^{'} }{\mathrm{1}^{{x}} \:+\mathrm{2}^{{x}} \:+\mathrm{3}^{{x}} \:+…+{n}^{{x}} }\:=\frac{\left(\mathrm{1}+{e}^{{xln}\left(\mathrm{2}\right)} \:+{e}^{{xln}\left(\mathrm{3}\right)} +…{e}^{{xln}\left({n}\right)} \right)^{'} }{\mathrm{1}^{{x}} \:+\mathrm{2}^{{x}} \:+\mathrm{3}^{{x}} \:+…+{n}^{{x}} } \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)\mathrm{2}^{{x}} \:+{ln}\left(\mathrm{3}\right)\mathrm{3}^{{x}} +…+{ln}\left({n}\right){n}^{{x}} }{\mathrm{1}^{{x}} \:+\mathrm{2}^{{x}} \:+\mathrm{3}^{{x}} \:+…+{n}^{{x}} }\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:{u}^{'} \left({x}\right)=\frac{{ln}\left(\mathrm{1}\right)+{ln}\left(\mathrm{2}\right)+…{ln}\left({n}\right)}{{n}}\:=\frac{{ln}\left({n}!\right)}{{n}}\:\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:{A}\left({x}\right)\:={e}^{\frac{{ln}\left({n}!\right)}{{n}}} \:=\left({e}^{{ln}\left({n}!\right)} \right)^{\frac{\mathrm{1}}{{n}}} \:=\left({n}!\right)^{\frac{\mathrm{1}}{{n}}} \\ $$
