Question Number 10515 by ABD last updated on 15/Feb/17
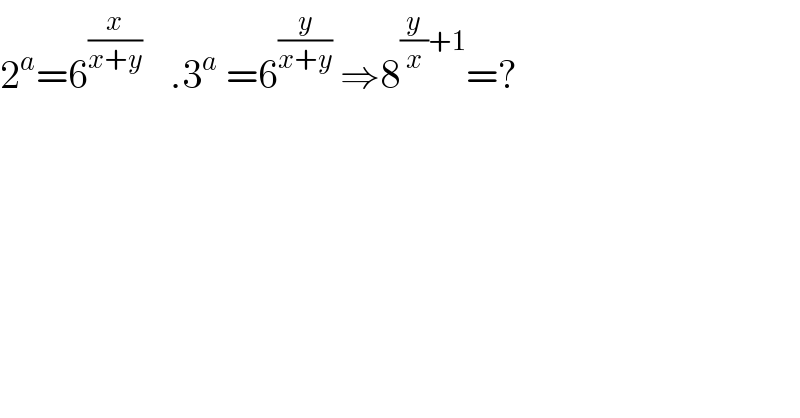
$$\mathrm{2}^{{a}} =\mathrm{6}^{\frac{{x}}{{x}+{y}}\:} \:\:\:.\mathrm{3}^{{a}} \:=\mathrm{6}^{\frac{{y}}{{x}+{y}}} \:\Rightarrow\mathrm{8}^{\frac{{y}}{{x}}+\mathrm{1}} =? \\ $$
Answered by mrW1 last updated on 15/Feb/17
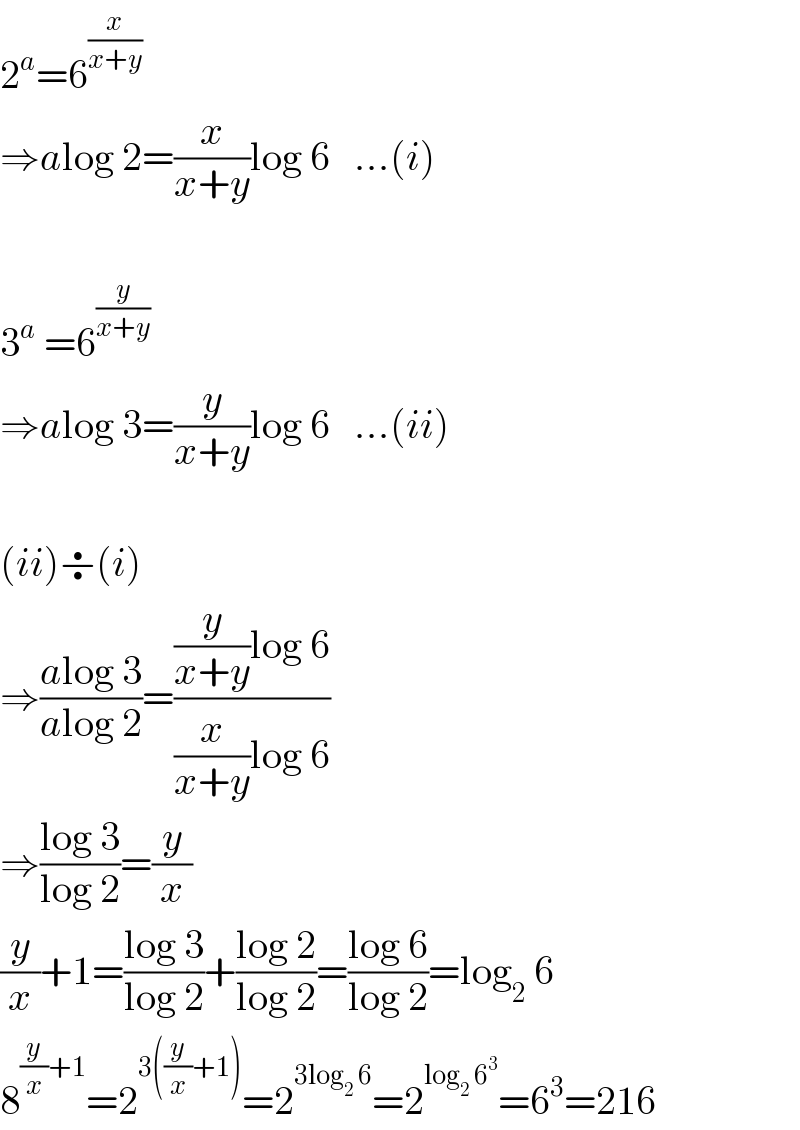
$$\mathrm{2}^{{a}} =\mathrm{6}^{\frac{{x}}{{x}+{y}}\:} \\ $$$$\Rightarrow{a}\mathrm{log}\:\mathrm{2}=\frac{{x}}{{x}+{y}}\mathrm{log}\:\mathrm{6}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\mathrm{3}^{{a}} \:=\mathrm{6}^{\frac{{y}}{{x}+{y}}} \\ $$$$\Rightarrow{a}\mathrm{log}\:\mathrm{3}=\frac{{y}}{{x}+{y}}\mathrm{log}\:\mathrm{6}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\left({ii}\right)\boldsymbol{\div}\left({i}\right) \\ $$$$\Rightarrow\frac{{a}\mathrm{log}\:\mathrm{3}}{{a}\mathrm{log}\:\mathrm{2}}=\frac{\frac{{y}}{{x}+{y}}\mathrm{log}\:\mathrm{6}}{\frac{{x}}{{x}+{y}}\mathrm{log}\:\mathrm{6}} \\ $$$$\Rightarrow\frac{\mathrm{log}\:\mathrm{3}}{\mathrm{log}\:\mathrm{2}}=\frac{{y}}{{x}} \\ $$$$\frac{{y}}{{x}}+\mathrm{1}=\frac{\mathrm{log}\:\mathrm{3}}{\mathrm{log}\:\mathrm{2}}+\frac{\mathrm{log}\:\mathrm{2}}{\mathrm{log}\:\mathrm{2}}=\frac{\mathrm{log}\:\mathrm{6}}{\mathrm{log}\:\mathrm{2}}=\mathrm{log}_{\mathrm{2}} \:\mathrm{6} \\ $$$$\mathrm{8}^{\frac{{y}}{{x}}+\mathrm{1}} =\mathrm{2}^{\mathrm{3}\left(\frac{{y}}{{x}}+\mathrm{1}\right)} =\mathrm{2}^{\mathrm{3log}_{\mathrm{2}} \:\mathrm{6}} =\mathrm{2}^{\mathrm{log}_{\mathrm{2}} \:\mathrm{6}^{\mathrm{3}} } =\mathrm{6}^{\mathrm{3}} =\mathrm{216} \\ $$
Commented by ajfour last updated on 16/Feb/17
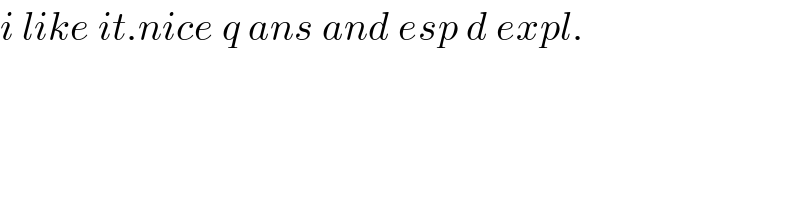
$${i}\:{like}\:{it}.{nice}\:{q}\:{ans}\:{and}\:{esp}\:{d}\:{expl}. \\ $$
