Question Number 141856 by rs4089 last updated on 24/May/21

Answered by TheSupreme last updated on 24/May/21
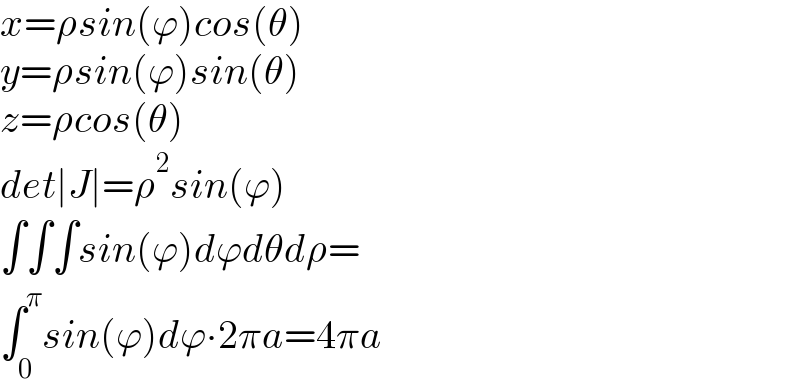
$${x}=\rho{sin}\left(\varphi\right){cos}\left(\theta\right) \\ $$$${y}=\rho{sin}\left(\varphi\right){sin}\left(\theta\right) \\ $$$${z}=\rho{cos}\left(\theta\right) \\ $$$${det}\mid{J}\mid=\rho^{\mathrm{2}} {sin}\left(\varphi\right) \\ $$$$\int\int\int{sin}\left(\varphi\right){d}\varphi{d}\theta{d}\rho= \\ $$$$\int_{\mathrm{0}} ^{\pi} {sin}\left(\varphi\right){d}\varphi\centerdot\mathrm{2}\pi{a}=\mathrm{4}\pi{a} \\ $$
