Question Number 10846 by Saham last updated on 27/Feb/17

$$\mathrm{Two}\:\mathrm{parallel}\:\mathrm{chords}\:\mathrm{of}\:\mathrm{length}\:\mathrm{24}\:\mathrm{cm}\:\mathrm{and}\:\mathrm{10}\:\mathrm{cm}\:\mathrm{which}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{opposite} \\ $$$$\mathrm{sides}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{are}\:\mathrm{17}\:\mathrm{cm}\:\mathrm{apart}.\:\mathrm{Calculate}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{nearest}\:\mathrm{whole}\:\mathrm{number}. \\ $$
Answered by mrW1 last updated on 27/Feb/17
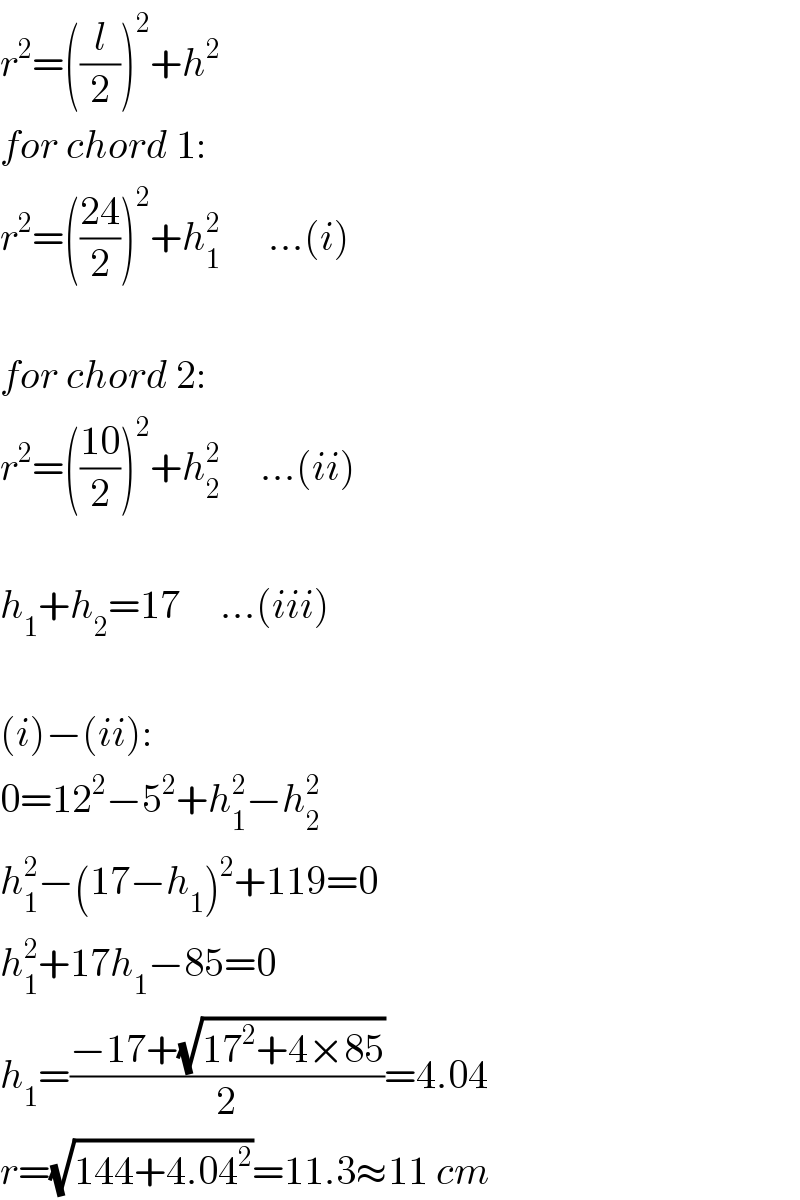
$${r}^{\mathrm{2}} =\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} \\ $$$${for}\:{chord}\:\mathrm{1}: \\ $$$${r}^{\mathrm{2}} =\left(\frac{\mathrm{24}}{\mathrm{2}}\right)^{\mathrm{2}} +{h}_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${for}\:{chord}\:\mathrm{2}: \\ $$$${r}^{\mathrm{2}} =\left(\frac{\mathrm{10}}{\mathrm{2}}\right)^{\mathrm{2}} +{h}_{\mathrm{2}} ^{\mathrm{2}} \:\:\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${h}_{\mathrm{1}} +{h}_{\mathrm{2}} =\mathrm{17}\:\:\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\mathrm{0}=\mathrm{12}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} +{h}_{\mathrm{1}} ^{\mathrm{2}} −{h}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${h}_{\mathrm{1}} ^{\mathrm{2}} −\left(\mathrm{17}−{h}_{\mathrm{1}} \right)^{\mathrm{2}} +\mathrm{119}=\mathrm{0} \\ $$$${h}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{17}{h}_{\mathrm{1}} −\mathrm{85}=\mathrm{0} \\ $$$${h}_{\mathrm{1}} =\frac{−\mathrm{17}+\sqrt{\mathrm{17}^{\mathrm{2}} +\mathrm{4}×\mathrm{85}}}{\mathrm{2}}=\mathrm{4}.\mathrm{04} \\ $$$${r}=\sqrt{\mathrm{144}+\mathrm{4}.\mathrm{04}^{\mathrm{2}} }=\mathrm{11}.\mathrm{3}\approx\mathrm{11}\:{cm} \\ $$
Commented by Saham last updated on 27/Feb/17

$$\mathrm{i}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
Commented by Saham last updated on 27/Feb/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
