Question Number 10902 by Nayon last updated on 01/Mar/17
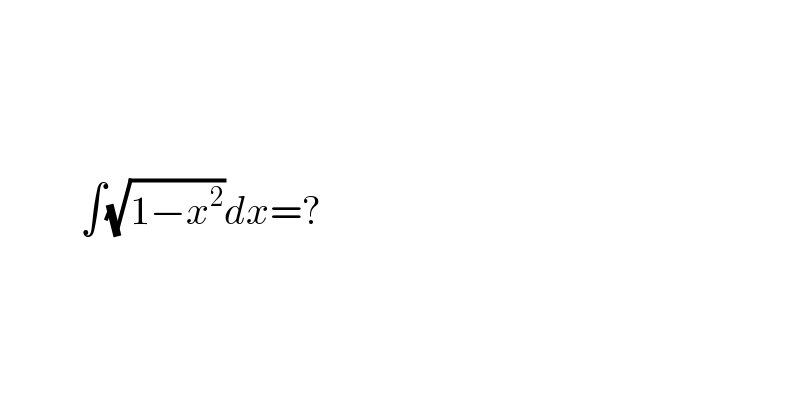
$$ \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\int\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=? \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by ridwan balatif last updated on 02/Mar/17

$$\int\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{let}:\:\mathrm{x}=\mathrm{sin}\theta\rightarrow\mathrm{cos}\theta=\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{dx}}{\mathrm{d}\theta}=\mathrm{cos}\theta \\ $$$$\:\:\:\:\:\:\:\mathrm{dx}=\mathrm{cos}\theta\:\mathrm{d}\theta \\ $$$$\int\sqrt{\mathrm{1}−\left(\mathrm{sin}\theta\right)^{\mathrm{2}} }\left(\mathrm{cos}\theta\right)\mathrm{d}\theta \\ $$$$\int\sqrt{\mathrm{cos}^{\mathrm{2}} \theta\:}×\mathrm{cos}\theta\mathrm{d}\theta \\ $$$$\int\mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\mathrm{Remember}:\: \\ $$$$\mathrm{cos2}\theta=−\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \theta \\ $$$$\mathrm{cos}^{\mathrm{2}} \theta\:=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos2}\theta\:!! \\ $$$$\int\mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta=\int\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos2}\theta\right)\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\theta+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin2}\theta+\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\theta+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\theta×\mathrm{cos}\theta+\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }+\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$
Commented by Nayon last updated on 01/Mar/17

$${wrong}\:{answer} \\ $$
Commented by sandy_suhendra last updated on 02/Mar/17
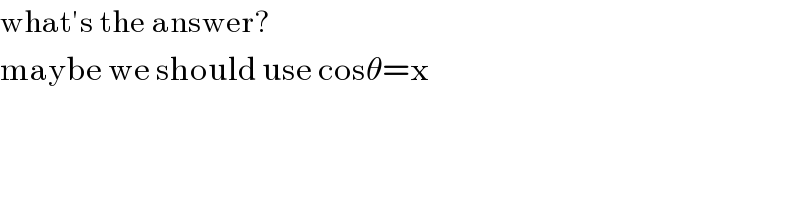
$$\mathrm{what}'\mathrm{s}\:\mathrm{the}\:\mathrm{answer}? \\ $$$$\mathrm{maybe}\:\mathrm{we}\:\mathrm{should}\:\mathrm{use}\:\mathrm{cos}\theta=\mathrm{x} \\ $$
Commented by prakash jain last updated on 03/Mar/17
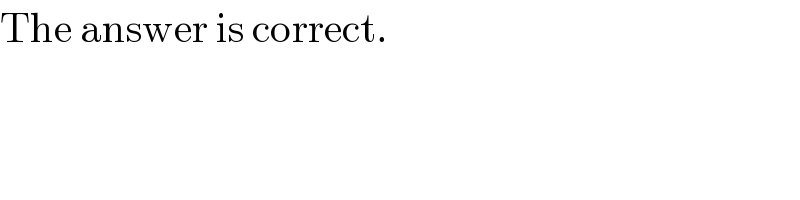
$$\mathrm{The}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{correct}.\: \\ $$
Answered by Abdulhalim Ghadady last updated on 02/Mar/17
![I=∫(√(1−x^2 ))dx=∫((1−x^2 )/( (√(1−x^2 ))))dx =∫(1/( (√(1−x^2 ))))dx−∫(x^2 /( (√(1−x^2 ))))dx =sin^(−1) x−∫((x.x)/( (√(1−x^2 ))))dx let: u=x u′=1 v^′ =(x/( (√(1−x^2 )))) v=−(√(1−x^2 )) I=sin^(−1) x−[−x(√(1−x^2 ))−∫−(√(1−x^2 ))dx] I=sin^(−1) x+x(√(1−x^2 ))−I 2I=sin^(−1) x+x(√(1−x^2 )) ∴I=(1/2)sin^(−1) x+(1/2)x(√(1−x^2 ))+C](https://www.tinkutara.com/question/Q10931.png)
$${I}=\int\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\int\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−\int\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\mathrm{sin}^{−\mathrm{1}} {x}−\int\frac{{x}.{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${let}: \\ $$$${u}={x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}'=\mathrm{1} \\ $$$${v}^{'} =\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:\:\:\:{v}=−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${I}=\mathrm{sin}^{−\mathrm{1}} {x}−\left[−{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\int−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\right] \\ $$$${I}=\mathrm{sin}^{−\mathrm{1}} {x}+{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−{I} \\ $$$$\mathrm{2}{I}=\mathrm{sin}^{−\mathrm{1}} {x}+{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\therefore{I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} {x}+\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{C} \\ $$
