Menu Close

Determine-x-e-y-x-1-i-1-y-i-i-10-1-xy-i-i-21-

Tinku Tara 0 Comments
Pin




Question Number 66431 by hmamarques1994@gmail.com last updated on 15/Aug/19
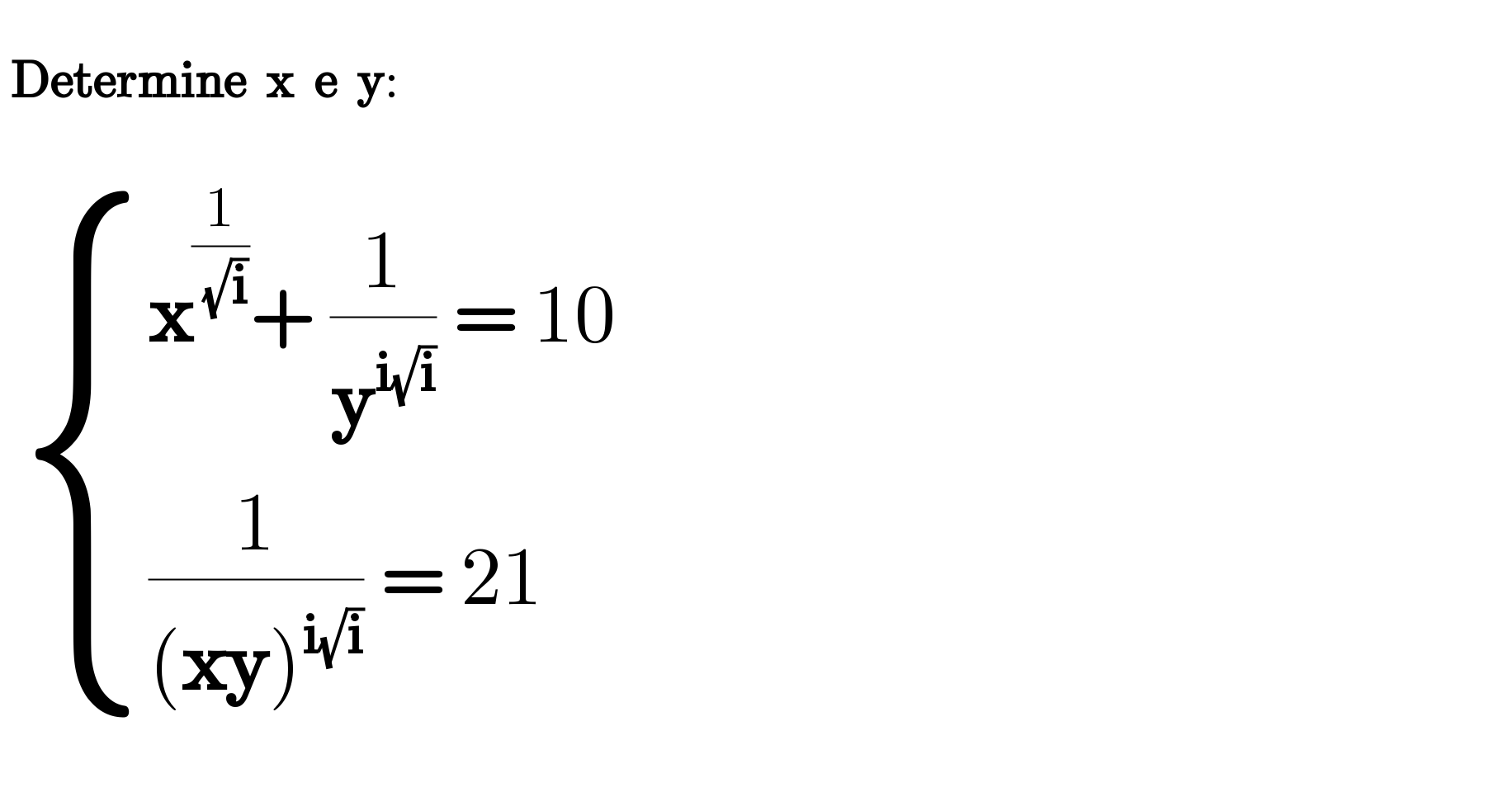
Determine x e y: { ((x^(1/( (√i))) + (1/y^(i(√i)) ) = 10)),(((1/((xy)^(i(√i)) )) = 21)) :}
$$\: \\ $$$$\:\boldsymbol{\mathrm{Determine}}\:\:\boldsymbol{\mathrm{x}}\:\:\boldsymbol{\mathrm{e}}\:\:\boldsymbol{\mathrm{y}}: \\ $$$$\: \\ $$$$\:\begin{cases}{\boldsymbol{\mathrm{x}}^{\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{\mathrm{i}}}}} +\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{y}}^{\boldsymbol{\mathrm{i}}\sqrt{\boldsymbol{\mathrm{i}}}} }\:=\:\mathrm{10}}\\{\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{xy}}\right)^{\boldsymbol{\mathrm{i}}\sqrt{\boldsymbol{\mathrm{i}}}} }\:=\:\mathrm{21}}\end{cases} \\ $$$$\: \\ $$
Answered by MJS last updated on 15/Aug/19
x^(1/( (√i))) =x^(((√2)/2)−((√2)/2)i) (1/y^(i(√i)) )=y^(((√2)/2)−((√2)/2)i) a+b=10 ab=21 ⇒ a=3∧b=7 ∨ a=7∧b=3 we have to solve z^(((√2)/2)−((√2)/2)i) =3 ⇒ z=3^((√2)/2) e^(i(((√2)ln 3)/2)) ≈1.55077+1.52444i z^(((√2)/2)−((√2)/2)i) =7 ⇒ z=7^((√2)/2) e^(i(((√2)ln 7)/2)) ≈.766442+3.88400i ∨z=7^((√2)/2) e^(π(√2)) e^(i(((√2)(ln 7 −2π))/2)) ≈−335.646−25.1114i solutions: x=3^((√2)/2) e^(i(((√2)ln 3)/2)) ∧y=7^((√2)/2) e^(i(((√2)ln 7)/2)) x=3^((√2)/2) e^(i(((√2)ln 3)/2)) ∧y=7^((√2)/2) e^(π(√2)) e^(i(((√2)(ln 7 −2π))/2)) and exchange x⇄y
$${x}^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{i}}}} ={x}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i}} \\ $$$$\frac{\mathrm{1}}{{y}^{\mathrm{i}\sqrt{\mathrm{i}}} }={y}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i}} \\ $$$${a}+{b}=\mathrm{10} \\ $$$${ab}=\mathrm{21} \\ $$$$\Rightarrow\:{a}=\mathrm{3}\wedge{b}=\mathrm{7}\:\vee\:{a}=\mathrm{7}\wedge{b}=\mathrm{3} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve} \\ $$$$ \\ $$$${z}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i}} =\mathrm{3}\:\Rightarrow\:{z}=\mathrm{3}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \mathrm{e}^{\mathrm{i}\frac{\sqrt{\mathrm{2}}\mathrm{ln}\:\mathrm{3}}{\mathrm{2}}} \approx\mathrm{1}.\mathrm{55077}+\mathrm{1}.\mathrm{52444i} \\ $$$$ \\ $$$${z}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i}} =\mathrm{7}\:\Rightarrow\:{z}=\mathrm{7}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \mathrm{e}^{\mathrm{i}\frac{\sqrt{\mathrm{2}}\mathrm{ln}\:\mathrm{7}}{\mathrm{2}}} \approx.\mathrm{766442}+\mathrm{3}.\mathrm{88400i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee{z}=\mathrm{7}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \mathrm{e}^{\pi\sqrt{\mathrm{2}}} \mathrm{e}^{\mathrm{i}\frac{\sqrt{\mathrm{2}}\left(\mathrm{ln}\:\mathrm{7}\:−\mathrm{2}\pi\right)}{\mathrm{2}}} \approx−\mathrm{335}.\mathrm{646}−\mathrm{25}.\mathrm{1114i} \\ $$$$ \\ $$$$\mathrm{solutions}: \\ $$$$ \\ $$$${x}=\mathrm{3}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \mathrm{e}^{\mathrm{i}\frac{\sqrt{\mathrm{2}}\mathrm{ln}\:\mathrm{3}}{\mathrm{2}}} \wedge{y}=\mathrm{7}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \mathrm{e}^{\mathrm{i}\frac{\sqrt{\mathrm{2}}\mathrm{ln}\:\mathrm{7}}{\mathrm{2}}} \\ $$$${x}=\mathrm{3}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \mathrm{e}^{\mathrm{i}\frac{\sqrt{\mathrm{2}}\mathrm{ln}\:\mathrm{3}}{\mathrm{2}}} \wedge{y}=\mathrm{7}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \mathrm{e}^{\pi\sqrt{\mathrm{2}}} \mathrm{e}^{\mathrm{i}\frac{\sqrt{\mathrm{2}}\left(\mathrm{ln}\:\mathrm{7}\:−\mathrm{2}\pi\right)}{\mathrm{2}}} \\ $$$$\mathrm{and}\:\mathrm{exchange}\:{x}\rightleftarrows{y} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *