Question Number 76438 by john santu last updated on 27/Dec/19
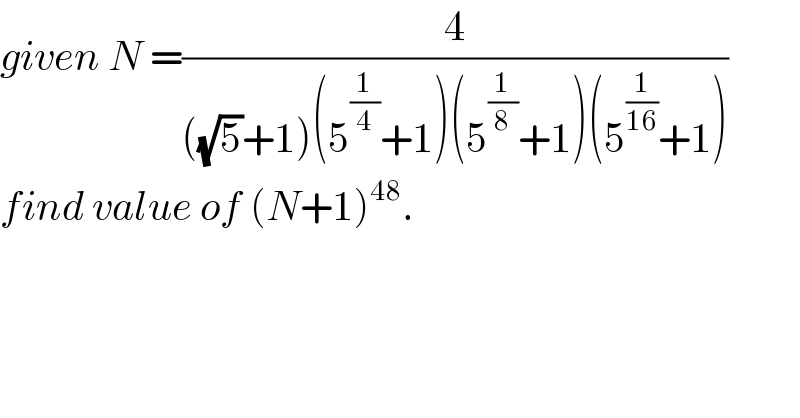
$${given}\:{N}\:=\frac{\mathrm{4}}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{8}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} +\mathrm{1}\right)} \\ $$$${find}\:{value}\:{of}\:\left({N}+\mathrm{1}\right)^{\mathrm{48}} . \\ $$
Answered by mr W last updated on 27/Dec/19
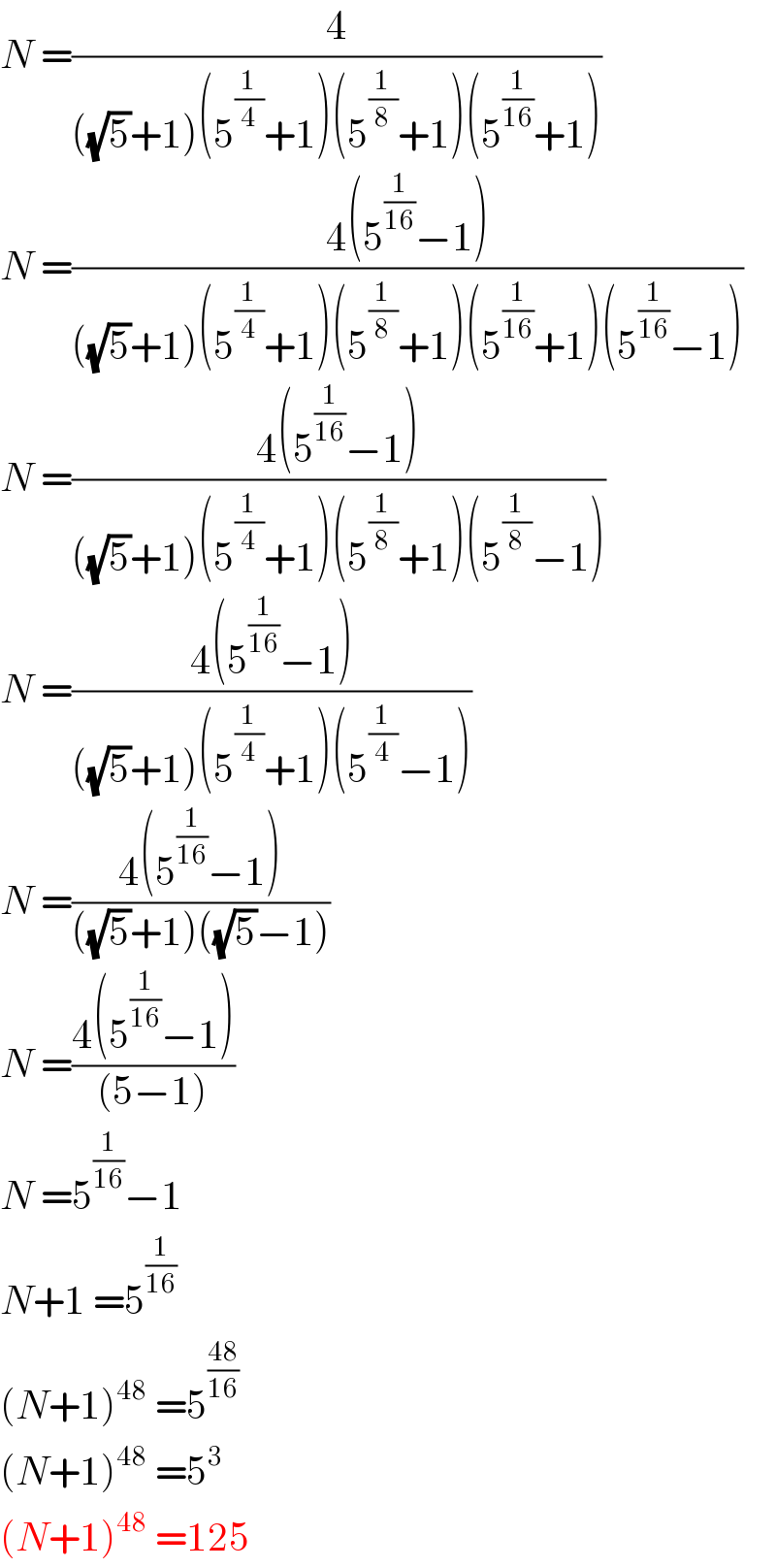
$${N}\:=\frac{\mathrm{4}}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{8}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} +\mathrm{1}\right)} \\ $$$${N}\:=\frac{\mathrm{4}\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right)}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{8}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right)} \\ $$$${N}\:=\frac{\mathrm{4}\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right)}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{8}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{8}}} −\mathrm{1}\right)} \\ $$$${N}\:=\frac{\mathrm{4}\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right)}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} −\mathrm{1}\right)} \\ $$$${N}\:=\frac{\mathrm{4}\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right)}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)} \\ $$$${N}\:=\frac{\mathrm{4}\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right)}{\left(\mathrm{5}−\mathrm{1}\right)} \\ $$$${N}\:=\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1} \\ $$$${N}+\mathrm{1}\:=\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{16}}} \\ $$$$\left({N}+\mathrm{1}\right)^{\mathrm{48}} \:=\mathrm{5}^{\frac{\mathrm{48}}{\mathrm{16}}} \\ $$$$\left({N}+\mathrm{1}\right)^{\mathrm{48}} \:=\mathrm{5}^{\mathrm{3}} \\ $$$$\left({N}+\mathrm{1}\right)^{\mathrm{48}} \:=\mathrm{125} \\ $$
Commented by john santu last updated on 28/Dec/19

$${thanks}\:{you}.\:{gbu}\: \\ $$
