Question Number 76445 by john santu last updated on 27/Dec/19
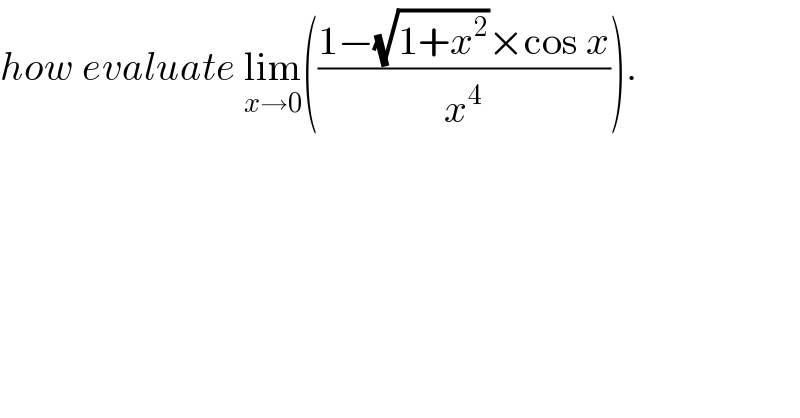
$${how}\:{evaluate}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }×\mathrm{cos}\:{x}}{{x}^{\mathrm{4}} }\right). \\ $$
Commented by JDamian last updated on 27/Dec/19
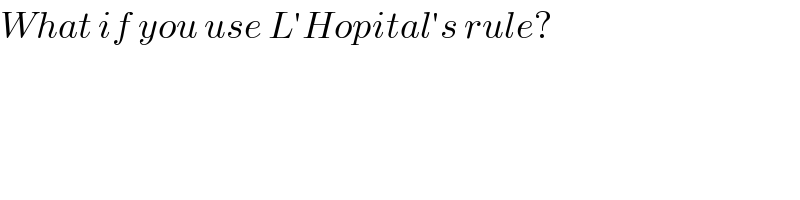
$${What}\:{if}\:{you}\:{use}\:{L}'{Hopital}'{s}\:{rule}? \\ $$
Commented by john santu last updated on 27/Dec/19
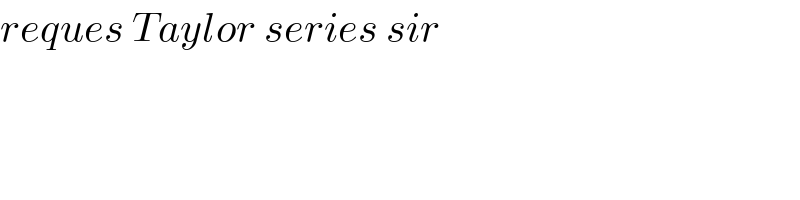
$${reques}\:{Taylor}\:{series}\:{sir} \\ $$
Commented by abdomathmax last updated on 27/Dec/19
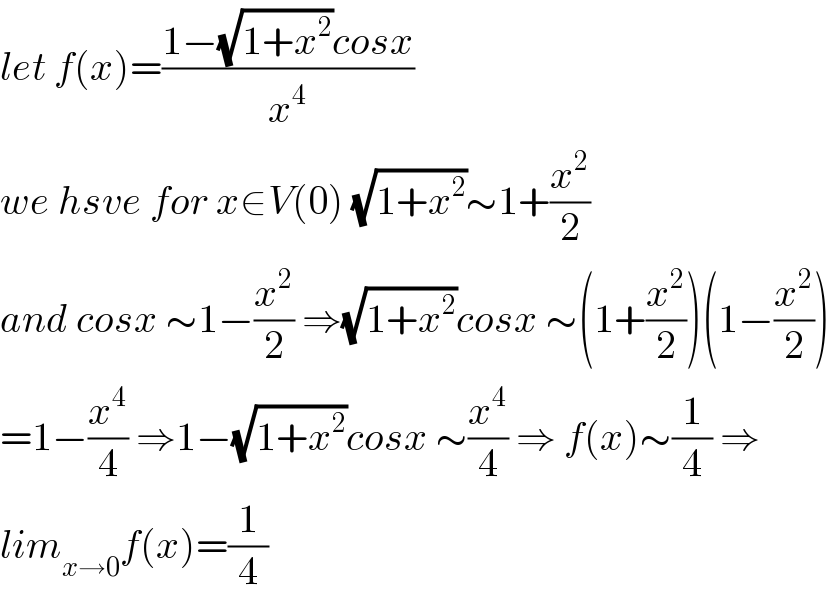
$${let}\:{f}\left({x}\right)=\frac{\mathrm{1}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{cosx}}{{x}^{\mathrm{4}} } \\ $$$${we}\:{hsve}\:{for}\:{x}\in{V}\left(\mathrm{0}\right)\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\sim\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${and}\:{cosx}\:\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{cosx}\:\sim\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$=\mathrm{1}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\:\Rightarrow\mathrm{1}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{cosx}\:\sim\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\:\Rightarrow\:{f}\left({x}\right)\sim\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by john santu last updated on 27/Dec/19
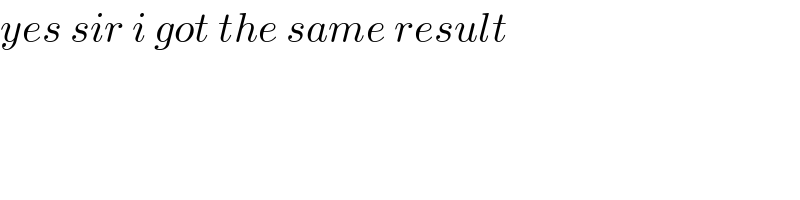
$${yes}\:{sir}\:{i}\:{got}\:{the}\:{same}\:{result} \\ $$
Commented by benjo last updated on 27/Dec/19
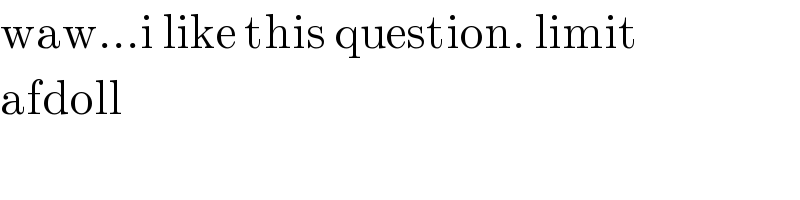
$$\mathrm{waw}…\mathrm{i}\:\mathrm{like}\:\mathrm{this}\:\mathrm{question}.\:\mathrm{limit} \\ $$$$\mathrm{afdoll} \\ $$
Commented by john santu last updated on 13/Jan/20
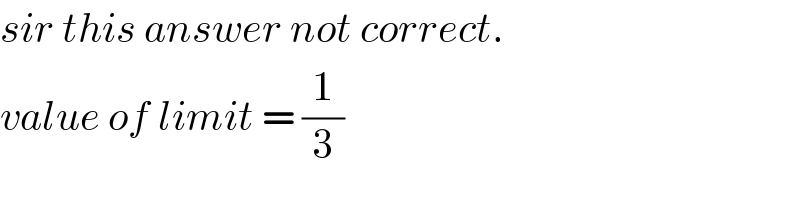
$${sir}\:{this}\:{answer}\:{not}\:{correct}.\: \\ $$$${value}\:{of}\:{limit}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
