Question Number 10913 by Saham last updated on 01/Mar/17
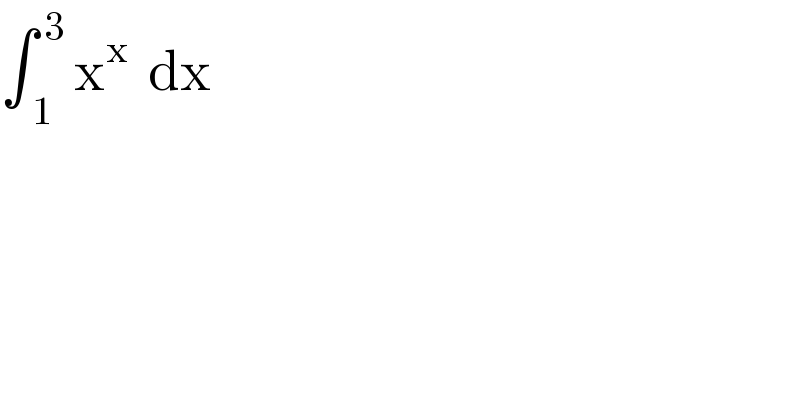
$$\int_{\:\mathrm{1}} ^{\:\mathrm{3}} \:\mathrm{x}^{\mathrm{x}} \:\:\mathrm{dx} \\ $$
Answered by FilupS last updated on 02/Mar/17
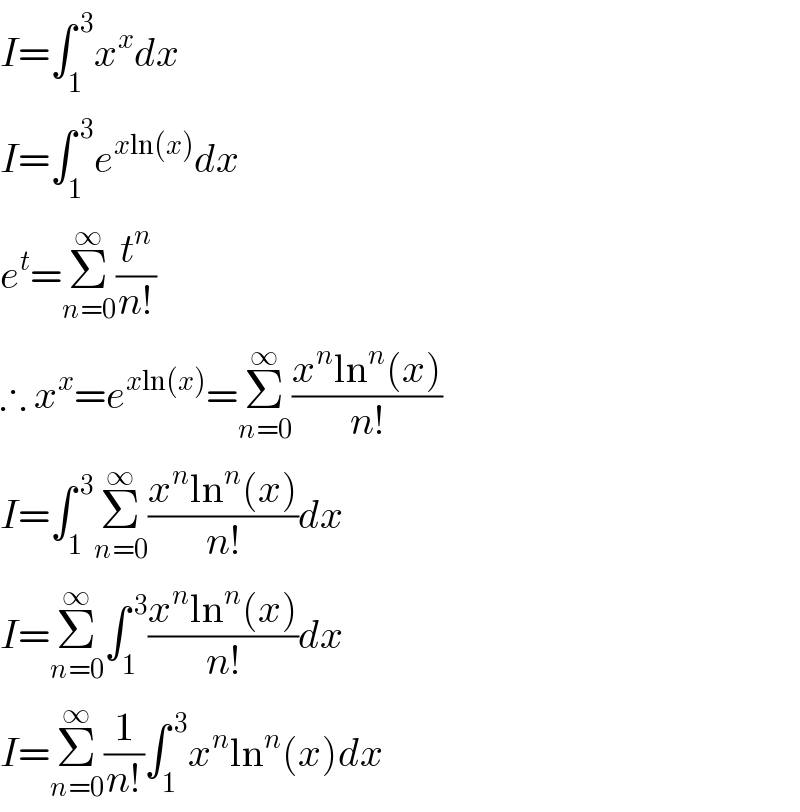
$${I}=\int_{\mathrm{1}} ^{\:\mathrm{3}} {x}^{{x}} {dx} \\ $$$${I}=\int_{\mathrm{1}} ^{\:\mathrm{3}} {e}^{{x}\mathrm{ln}\left({x}\right)} {dx} \\ $$$${e}^{{t}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{t}^{{n}} }{{n}!} \\ $$$$\therefore\:{x}^{{x}} ={e}^{{x}\mathrm{ln}\left({x}\right)} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} \mathrm{ln}^{{n}} \left({x}\right)}{{n}!} \\ $$$${I}=\int_{\mathrm{1}} ^{\:\mathrm{3}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} \mathrm{ln}^{{n}} \left({x}\right)}{{n}!}{dx} \\ $$$${I}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{1}} ^{\:\mathrm{3}} \frac{{x}^{{n}} \mathrm{ln}^{{n}} \left({x}\right)}{{n}!}{dx} \\ $$$${I}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int_{\mathrm{1}} ^{\:\mathrm{3}} {x}^{{n}} \mathrm{ln}^{{n}} \left({x}\right){dx} \\ $$
Commented by Saham last updated on 02/Mar/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
