Question Number 141997 by jlewis last updated on 25/May/21

$$\mathrm{find}\:\mathrm{two}\:\mathrm{irrational}\:\mathrm{numbers}\: \\ $$$$\mathrm{between}\:\mathrm{0}.\mathrm{333}….\:\mathrm{and}\:\mathrm{0}.\mathrm{444}… \\ $$$$ \\ $$
Answered by MJS_new last updated on 25/May/21

$$.\mathrm{33312345678910111213}… \\ $$$$\frac{\mathrm{1}}{\mathrm{e}}\approx.\mathrm{367879441}… \\ $$
Commented by MJS_new last updated on 25/May/21

$$.\mathrm{333000333300003333300000}… \\ $$
Commented by jlewis last updated on 25/May/21

$$\mathrm{wah}!\:\mathrm{i}\:\mathrm{have}\:\mathrm{not}\:\mathrm{gotten}\:\mathrm{how}\:\mathrm{u} \\ $$$$\:\mathrm{arrived}\:\mathrm{to}\:\mathrm{this} \\ $$
Commented by MJS_new last updated on 25/May/21

$$\mathrm{easy}:\:\mathrm{invent}\:\mathrm{an}\:\mathrm{infinite}\:\mathrm{non}−\mathrm{periodic}\:\mathrm{pattern} \\ $$$$.\mathrm{01}\:\mathrm{001}\:\mathrm{0001}\:\mathrm{00001}\:\mathrm{000001}… \\ $$$$.\mathrm{0}\:\mathrm{1}\:\mathrm{2}\:\mathrm{3}\:\mathrm{4}\:\mathrm{5}\:\mathrm{6}\:\mathrm{7}\:\mathrm{8}\:\mathrm{9}\:\mathrm{10}\:\mathrm{11}\:\mathrm{12}… \\ $$$$.\mathrm{1}\:\mathrm{4}\:\mathrm{9}\:\mathrm{16}\:\mathrm{25}\:\mathrm{36}\:\mathrm{49}\:\mathrm{64}\:\mathrm{81}\:\mathrm{100}… \\ $$$$.\mathrm{2}\:\mathrm{4}\:\mathrm{8}\:\mathrm{16}\:\mathrm{32}\:\mathrm{64}\:\mathrm{128}\:\mathrm{256}\:\mathrm{512}… \\ $$$$.\mathrm{0}\:\mathrm{1}\:\mathrm{1}\:\mathrm{2}\:\mathrm{3}\:\mathrm{5}\:\mathrm{8}\:\mathrm{13}\:\mathrm{21}\:\mathrm{34}\:\mathrm{55}\:\mathrm{89}… \\ $$
Commented by jlewis last updated on 25/May/21
$$\:\mathrm{i}\:\mathrm{get}\:\mathrm{it}\:\mathrm{now}.\mathrm{thanks} \\ $$
Answered by MJS_new last updated on 25/May/21
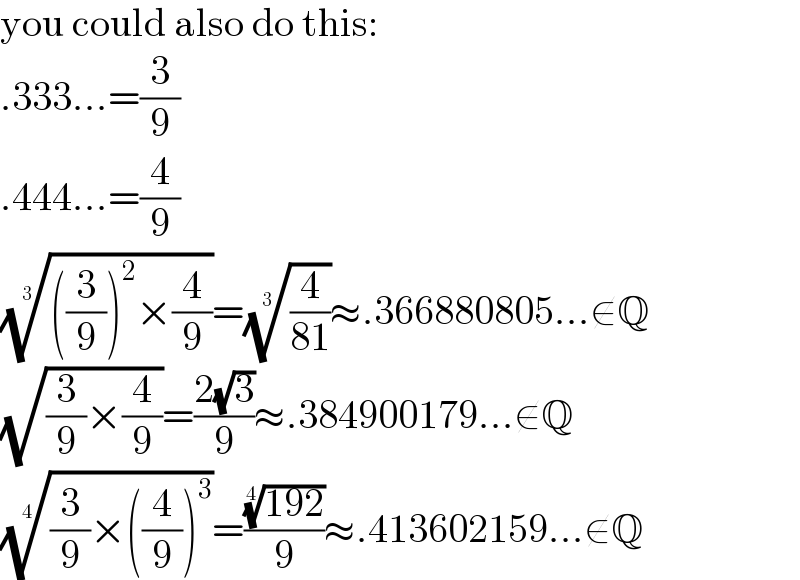
$$\mathrm{you}\:\mathrm{could}\:\mathrm{also}\:\mathrm{do}\:\mathrm{this}: \\ $$$$.\mathrm{333}…=\frac{\mathrm{3}}{\mathrm{9}} \\ $$$$.\mathrm{444}…=\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\sqrt[{\mathrm{3}}]{\left(\frac{\mathrm{3}}{\mathrm{9}}\right)^{\mathrm{2}} ×\frac{\mathrm{4}}{\mathrm{9}}}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{4}}{\mathrm{81}}}\approx.\mathrm{366880805}…\notin\mathbb{Q} \\ $$$$\sqrt{\frac{\mathrm{3}}{\mathrm{9}}×\frac{\mathrm{4}}{\mathrm{9}}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\approx.\mathrm{384900179}…\notin\mathbb{Q} \\ $$$$\sqrt[{\mathrm{4}}]{\frac{\mathrm{3}}{\mathrm{9}}×\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{\mathrm{3}} }=\frac{\sqrt[{\mathrm{4}}]{\mathrm{192}}}{\mathrm{9}}\approx.\mathrm{413602159}…\notin\mathbb{Q} \\ $$
