Question Number 76465 by kaivan.ahmadi last updated on 27/Dec/19
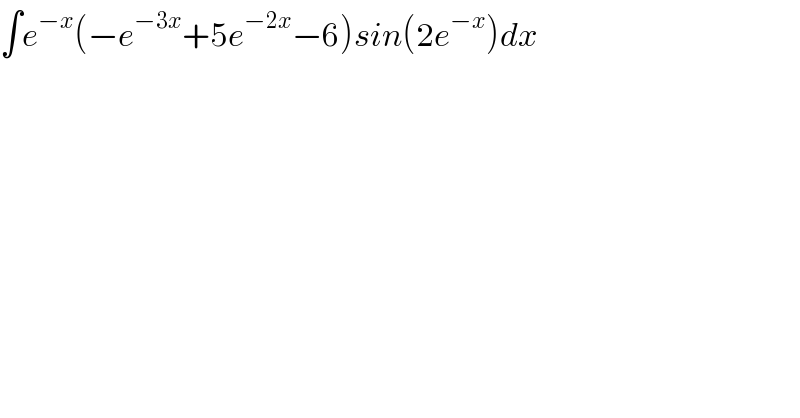
$$\int{e}^{−{x}} \left(−{e}^{−\mathrm{3}{x}} +\mathrm{5}{e}^{−\mathrm{2}{x}} −\mathrm{6}\right){sin}\left(\mathrm{2}{e}^{−{x}} \right){dx} \\ $$
Answered by john santu last updated on 28/Dec/19
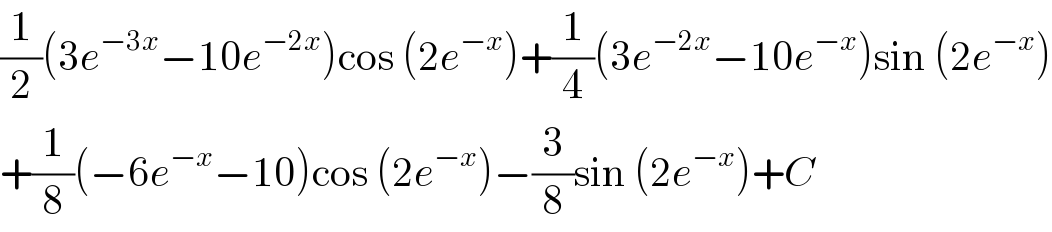
$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{e}^{−\mathrm{3}{x}} −\mathrm{10}{e}^{−\mathrm{2}{x}} \right)\mathrm{cos}\:\left(\mathrm{2}{e}^{−{x}} \right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}{e}^{−\mathrm{2}{x}} −\mathrm{10}{e}^{−{x}} \right)\mathrm{sin}\:\left(\mathrm{2}{e}^{−{x}} \right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{8}}\left(−\mathrm{6}{e}^{−{x}} −\mathrm{10}\right)\mathrm{cos}\:\left(\mathrm{2}{e}^{−{x}} \right)−\frac{\mathrm{3}}{\mathrm{8}}\mathrm{sin}\:\left(\mathrm{2}{e}^{−{x}} \right)+{C} \\ $$
