Question Number 10933 by Joel576 last updated on 02/Mar/17

$$\mathrm{If}\:\:{p}\:\:\mathrm{and}\:\:{q}\:\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{for}\:\mathrm{the} \\ $$$${x}^{\mathrm{2}} \:−\:\left({a}\:+\:\mathrm{1}\right){x}\:+\:\left(−{a}\:−\:\frac{\mathrm{5}}{\mathrm{2}}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\:{p}^{\mathrm{2}\:} +\:{q}^{\mathrm{2}} \:\:\mathrm{is}\:… \\ $$
Answered by ridwan balatif last updated on 02/Mar/17
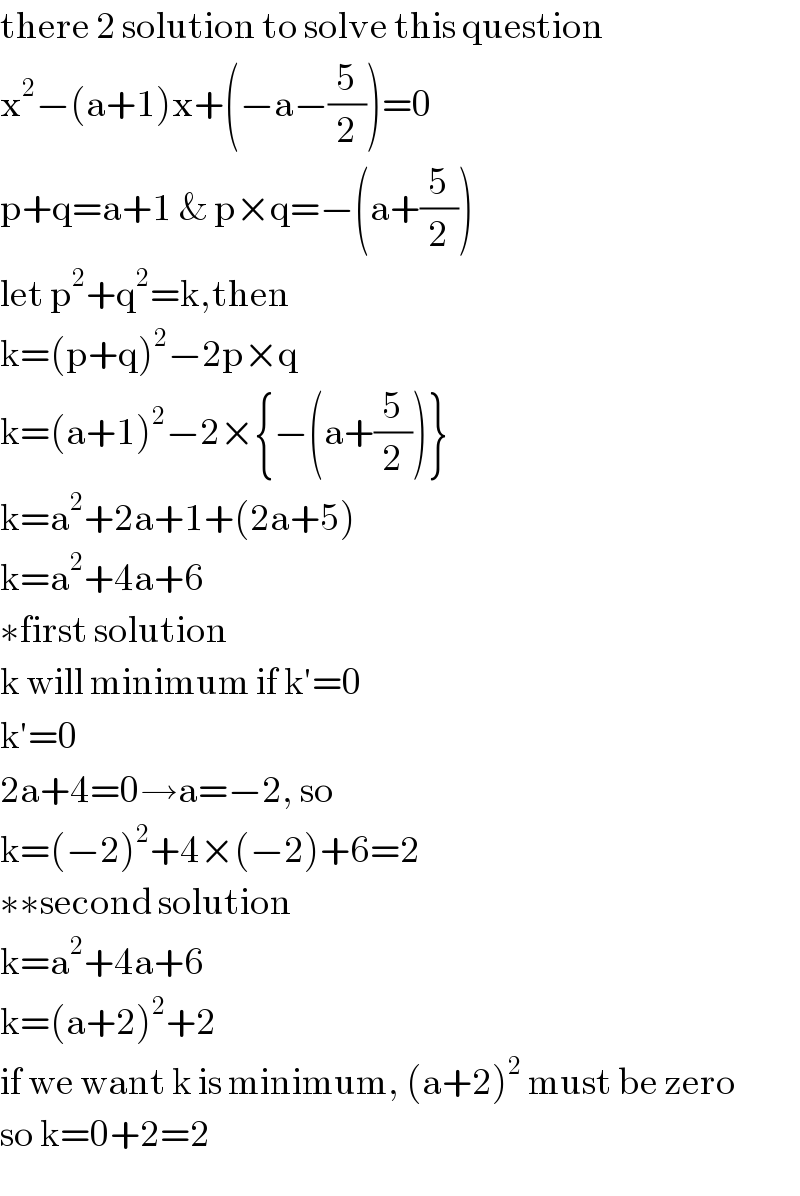
$$\mathrm{there}\:\mathrm{2}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{question} \\ $$$$\mathrm{x}^{\mathrm{2}} −\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}+\left(−\mathrm{a}−\frac{\mathrm{5}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{p}+\mathrm{q}=\mathrm{a}+\mathrm{1}\:\&\:\mathrm{p}×\mathrm{q}=−\left(\mathrm{a}+\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$\mathrm{let}\:\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} =\mathrm{k},\mathrm{then} \\ $$$$\mathrm{k}=\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} −\mathrm{2p}×\mathrm{q} \\ $$$$\mathrm{k}=\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}×\left\{−\left(\mathrm{a}+\frac{\mathrm{5}}{\mathrm{2}}\right)\right\} \\ $$$$\mathrm{k}=\mathrm{a}^{\mathrm{2}} +\mathrm{2a}+\mathrm{1}+\left(\mathrm{2a}+\mathrm{5}\right) \\ $$$$\mathrm{k}=\mathrm{a}^{\mathrm{2}} +\mathrm{4a}+\mathrm{6} \\ $$$$\ast\mathrm{first}\:\mathrm{solution} \\ $$$$\mathrm{k}\:\mathrm{will}\:\mathrm{minimum}\:\mathrm{if}\:\mathrm{k}'=\mathrm{0} \\ $$$$\mathrm{k}'=\mathrm{0} \\ $$$$\mathrm{2a}+\mathrm{4}=\mathrm{0}\rightarrow\mathrm{a}=−\mathrm{2},\:\mathrm{so} \\ $$$$\mathrm{k}=\left(−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4}×\left(−\mathrm{2}\right)+\mathrm{6}=\mathrm{2} \\ $$$$\ast\ast\mathrm{second}\:\mathrm{solution} \\ $$$$\mathrm{k}=\mathrm{a}^{\mathrm{2}} +\mathrm{4a}+\mathrm{6} \\ $$$$\mathrm{k}=\left(\mathrm{a}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{want}\:\mathrm{k}\:\mathrm{is}\:\mathrm{minimum},\:\left(\mathrm{a}+\mathrm{2}\right)^{\mathrm{2}} \:\mathrm{must}\:\mathrm{be}\:\mathrm{zero} \\ $$$$\mathrm{so}\:\mathrm{k}=\mathrm{0}+\mathrm{2}=\mathrm{2} \\ $$
Commented by Joel576 last updated on 02/Mar/17

$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by Joel576 last updated on 02/Mar/17

$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by bahmanfeshki last updated on 02/Mar/17

$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} ={S}^{\mathrm{2}} −\mathrm{2}{P}=\left({a}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{5}={a}^{\mathrm{2}} +\mathrm{4}{a}+\mathrm{6} \\ $$$${minimum}\:{value}=\frac{\mathrm{4}×\mathrm{1}×\mathrm{6}−\mathrm{4}^{\mathrm{2}} }{\mathrm{4}×\mathrm{1}}=\mathrm{2} \\ $$
