Question Number 76477 by mathocean1 last updated on 27/Dec/19
![Hello Solve in ]−π;π[ ((2sinx)/(cosx−sinx))≥0 result should be in radian please help me ...](https://www.tinkutara.com/question/Q76477.png)
$$\mathrm{Hello}\:\mathrm{Solve}\:\mathrm{in}\: \\ $$$$\left.\right]−\pi;\pi\left[\right. \\ $$$$\frac{\mathrm{2sin}{x}}{{cosx}−{sinx}}\geqslant\mathrm{0} \\ $$$$\mathrm{result}\:\mathrm{should}\:\mathrm{be}\:\mathrm{in}\:\mathrm{radian} \\ $$$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:… \\ $$
Answered by Kunal12588 last updated on 27/Dec/19
![((2sin x)/(cos x−sin x))=(((√2)sin x)/(sin((π/4)−x)))≥0 ⇒x∈[0,(π/4))∪(−((3π)/4),−π]](https://www.tinkutara.com/question/Q76478.png)
$$\frac{\mathrm{2}{sin}\:{x}}{{cos}\:{x}−{sin}\:{x}}=\frac{\sqrt{\mathrm{2}}{sin}\:{x}}{{sin}\left(\frac{\pi}{\mathrm{4}}−{x}\right)}\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}\in\left[\mathrm{0},\frac{\pi}{\mathrm{4}}\right)\cup\left(−\frac{\mathrm{3}\pi}{\mathrm{4}},−\pi\right] \\ $$
Commented by mathocean1 last updated on 27/Dec/19
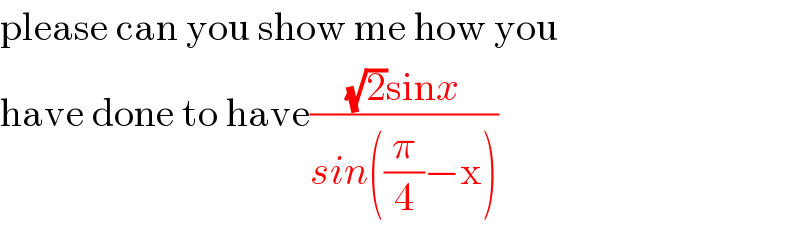
$$\mathrm{please}\:\mathrm{can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{me}\:\mathrm{how}\:\mathrm{you} \\ $$$$\mathrm{have}\:\mathrm{done}\:\mathrm{to}\:\mathrm{have}\frac{\sqrt{\mathrm{2}}\mathrm{sin}{x}}{{sin}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)} \\ $$
Commented by Kunal12588 last updated on 27/Dec/19
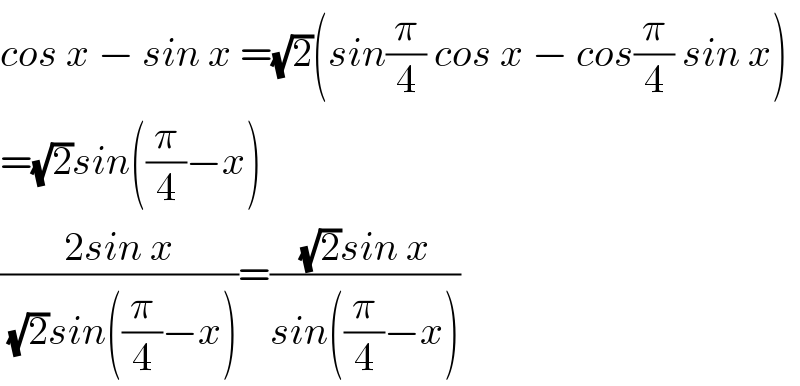
$${cos}\:{x}\:−\:{sin}\:{x}\:=\sqrt{\mathrm{2}}\left({sin}\frac{\pi}{\mathrm{4}}\:{cos}\:{x}\:−\:{cos}\frac{\pi}{\mathrm{4}}\:{sin}\:{x}\right) \\ $$$$=\sqrt{\mathrm{2}}{sin}\left(\frac{\pi}{\mathrm{4}}−{x}\right) \\ $$$$\frac{\mathrm{2}{sin}\:{x}}{\:\sqrt{\mathrm{2}}{sin}\left(\frac{\pi}{\mathrm{4}}−{x}\right)}=\frac{\sqrt{\mathrm{2}}{sin}\:{x}}{{sin}\left(\frac{\pi}{\mathrm{4}}−{x}\right)} \\ $$
Commented by mathocean1 last updated on 27/Dec/19
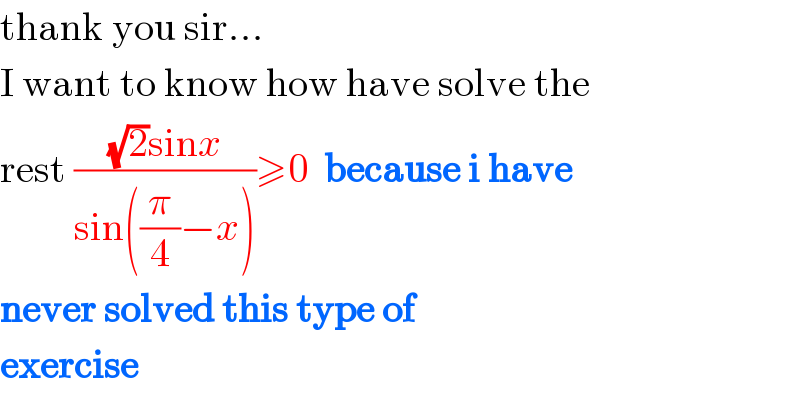
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}… \\ $$$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{how}\:\mathrm{have}\:\mathrm{solve}\:\mathrm{the} \\ $$$$\mathrm{rest}\:\frac{\sqrt{\mathrm{2}}\mathrm{sin}{x}}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−{x}\right)}\geqslant\mathrm{0}\:\:\boldsymbol{\mathrm{because}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{have}} \\ $$$$\boldsymbol{\mathrm{never}}\:\boldsymbol{\mathrm{solved}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{type}}\:\boldsymbol{\mathrm{of}}\: \\ $$$$\boldsymbol{\mathrm{exercise}}\: \\ $$
Commented by Kunal12588 last updated on 27/Dec/19

$${well}\:{I}\:{have}\:{also}\:{not}\:{solve}\:{such}\:{type}\:{of}\:{questions} \\ $$$${I}\:{just}\:{thought}\:{of}\:{an}\:{idea}\:{that}\:{if}\:{numerator} \\ $$$${is}\:{greater}\:{than}\:\mathrm{0}\:{then}\:{denominator}\:{should} \\ $$$${also}\:{be}\:{greater}\:{than}\:\mathrm{0}\:{similarly},\:{when}\:{N}_{{r}} <\mathrm{0} \\ $$$${then}\:{D}_{{r}} <\mathrm{0}. \\ $$
Commented by mathocean1 last updated on 27/Dec/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{once}\:\mathrm{more}\:\mathrm{sir}…\:\mathrm{may}\:\mathrm{God} \\ $$$$\mathrm{bless}\:\mathrm{you}… \\ $$$$\mathrm{By}\:\mathrm{the}\:\mathrm{way},\:\mathrm{i}\:\mathrm{wish}\:\mathrm{you}\:\mathrm{a}\:\mathrm{happy} \\ $$$$\mathrm{new}\:\mathrm{year}! \\ $$
Answered by MJS last updated on 27/Dec/19
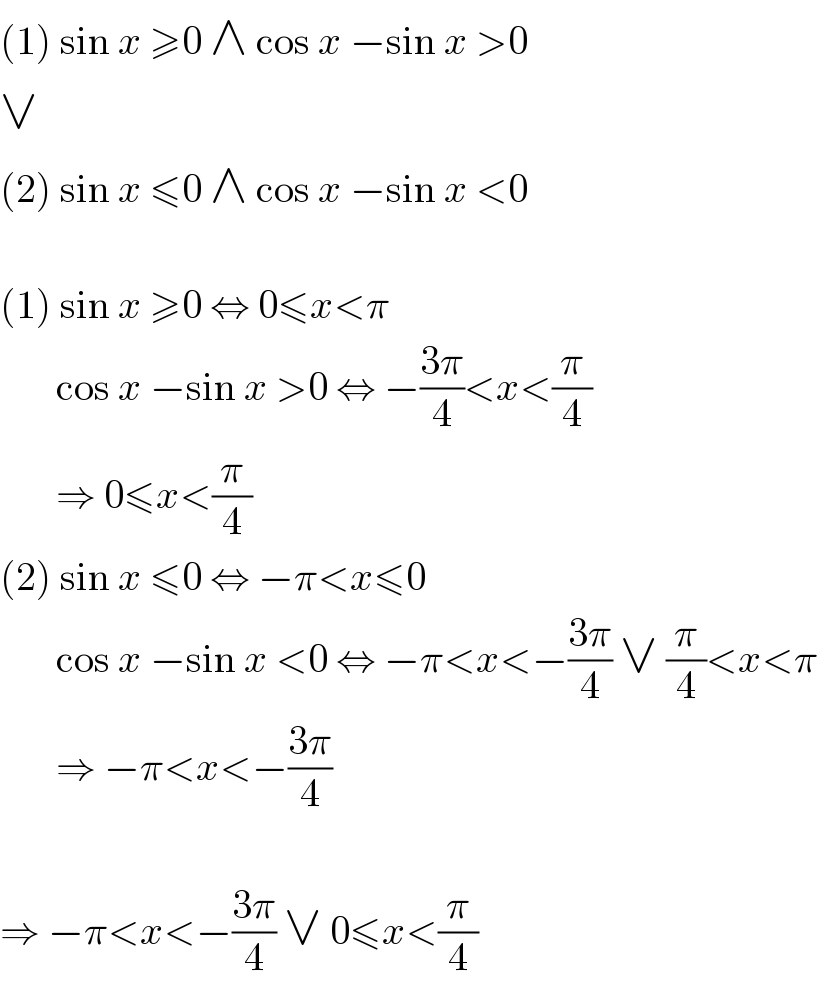
$$\left(\mathrm{1}\right)\:\mathrm{sin}\:{x}\:\geqslant\mathrm{0}\:\wedge\:\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\:>\mathrm{0} \\ $$$$\vee \\ $$$$\left(\mathrm{2}\right)\:\mathrm{sin}\:{x}\:\leqslant\mathrm{0}\:\wedge\:\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\:<\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{sin}\:{x}\:\geqslant\mathrm{0}\:\Leftrightarrow\:\mathrm{0}\leqslant{x}<\pi \\ $$$$\:\:\:\:\:\:\:\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\:>\mathrm{0}\:\Leftrightarrow\:−\frac{\mathrm{3}\pi}{\mathrm{4}}<{x}<\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\mathrm{0}\leqslant{x}<\frac{\pi}{\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{sin}\:{x}\:\leqslant\mathrm{0}\:\Leftrightarrow\:−\pi<{x}\leqslant\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\:<\mathrm{0}\:\Leftrightarrow\:−\pi<{x}<−\frac{\mathrm{3}\pi}{\mathrm{4}}\:\vee\:\frac{\pi}{\mathrm{4}}<{x}<\pi \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:−\pi<{x}<−\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$ \\ $$$$\Rightarrow\:−\pi<{x}<−\frac{\mathrm{3}\pi}{\mathrm{4}}\:\vee\:\mathrm{0}\leqslant{x}<\frac{\pi}{\mathrm{4}} \\ $$
Commented by mr W last updated on 28/Dec/19

$${x}=\pi\:{is}\:{missing}. \\ $$
Commented by MJS last updated on 28/Dec/19
![he typed ]−π; π[ ⇔ −π<x<π](https://www.tinkutara.com/question/Q76552.png)
$$\left.\mathrm{he}\:\mathrm{typed}\:\right]−\pi;\:\pi\left[\:\Leftrightarrow\:−\pi<{x}<\pi\right. \\ $$
