Question Number 76497 by mathmax by abdo last updated on 27/Dec/19

$${calculate}\:{tan}\left(\mathrm{3}{x}\right)\:{interms}\:{of}\:{tanx} \\ $$
Answered by Rio Michael last updated on 27/Dec/19
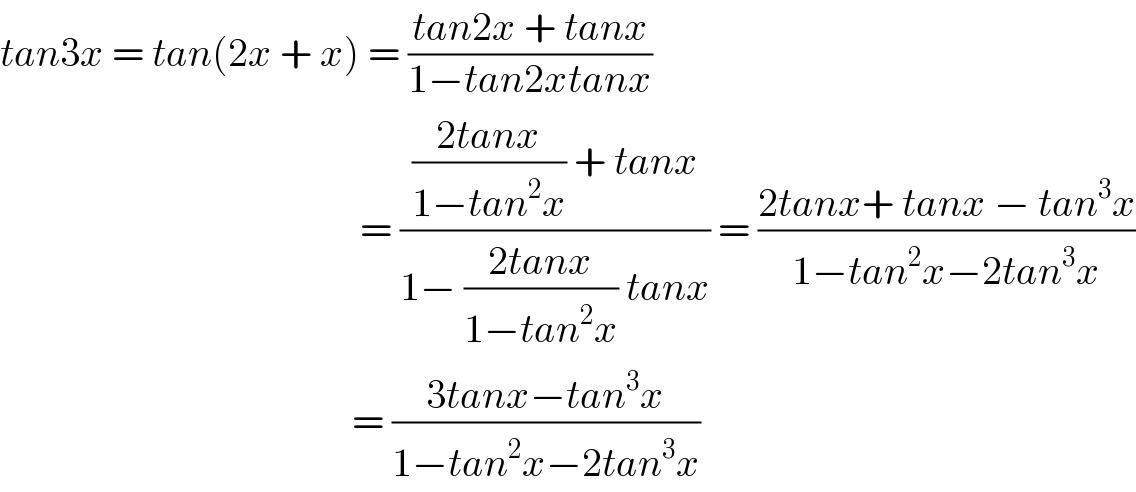
$${tan}\mathrm{3}{x}\:=\:{tan}\left(\mathrm{2}{x}\:+\:{x}\right)\:=\:\frac{{tan}\mathrm{2}{x}\:+\:{tanx}}{\mathrm{1}−{tan}\mathrm{2}{xtanx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\:+\:{tanx}}{\mathrm{1}−\:\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\:{tanx}}\:=\:\frac{\mathrm{2}{tanx}+\:{tanx}\:−\:{tan}^{\mathrm{3}} {x}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}−\mathrm{2}{tan}^{\mathrm{3}} {x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{3}{tanx}−{tan}^{\mathrm{3}} {x}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}−\mathrm{2}{tan}^{\mathrm{3}} {x}} \\ $$
Commented by mathmax by abdo last updated on 27/Dec/19

$${thankx}\:{sir}. \\ $$
Commented by MJS last updated on 27/Dec/19
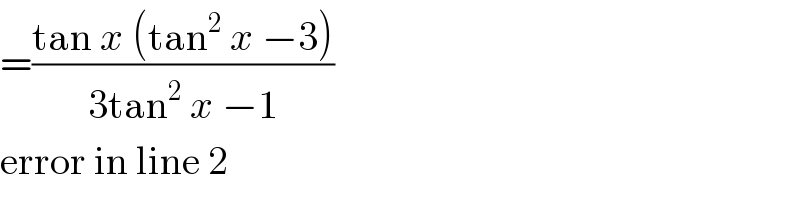
$$=\frac{\mathrm{tan}\:{x}\:\left(\mathrm{tan}^{\mathrm{2}} \:{x}\:−\mathrm{3}\right)}{\mathrm{3tan}^{\mathrm{2}} \:{x}\:−\mathrm{1}} \\ $$$$\mathrm{error}\:\mathrm{in}\:\mathrm{line}\:\mathrm{2} \\ $$
Answered by $@ty@m123 last updated on 28/Dec/19

$$\mathrm{tan}\:\mathrm{3}{x}=\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{cos}\:\mathrm{3}{x}} \\ $$$$=\frac{\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x}}{\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x}} \\ $$$$=\frac{\left(\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x}\right)\boldsymbol{\div}\mathrm{cos}\:^{\mathrm{3}} {x}}{\left(\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x}\right)\boldsymbol{\div}\mathrm{cos}\:^{\mathrm{3}} {x}} \\ $$$$=\frac{\mathrm{3tan}\:{x}.\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{4tan}\:^{\mathrm{3}} {x}}{\mathrm{4}−\mathrm{3sec}\:^{\mathrm{2}} {x}} \\ $$$$=\frac{\mathrm{3tan}\:{x}.\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)−\mathrm{4tan}\:^{\mathrm{3}} {x}}{\mathrm{4}−\mathrm{3}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)} \\ $$$$=\frac{\mathrm{3tan}\:{x}+\mathrm{3tan}\:^{\mathrm{3}} {x}−\mathrm{4tan}\:^{\mathrm{3}} {x}}{\mathrm{4}−\mathrm{3}−\mathrm{3tan}\:^{\mathrm{2}} {x}} \\ $$$$=\frac{\mathrm{3tan}\:{x}−\mathrm{tan}\:^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} {x}} \\ $$
