Question-142041

Question Number 142041 by nadovic last updated on 25/May/21

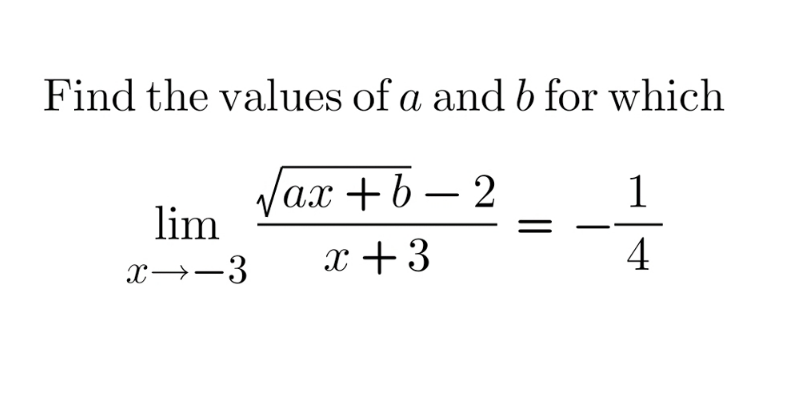
Answered by TheSupreme last updated on 25/May/21

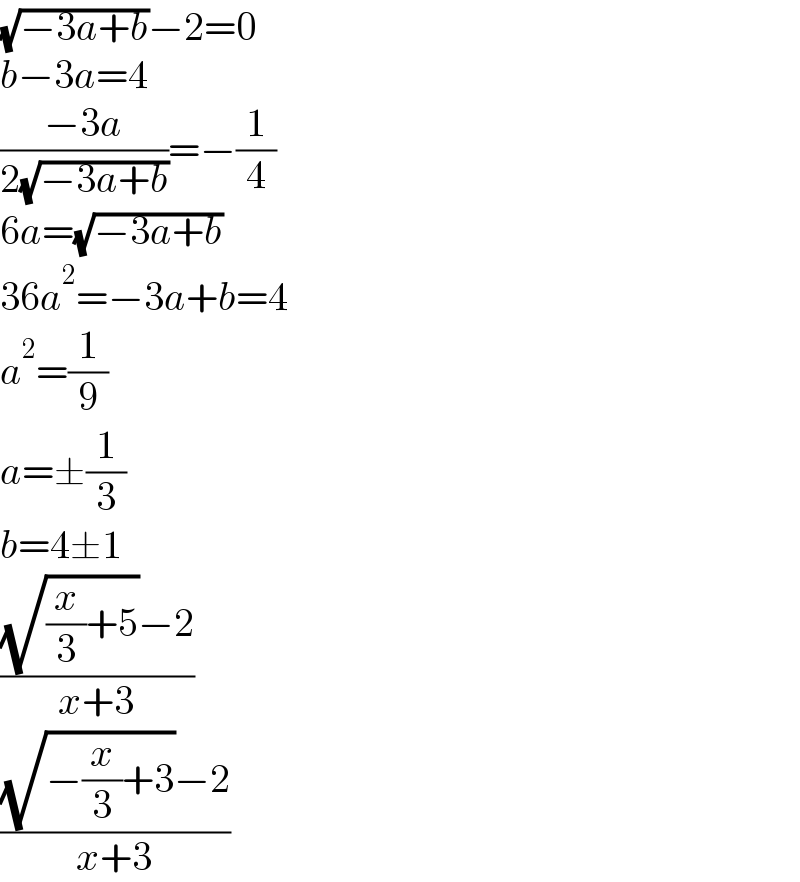
(√(−3a+b))−2=0 b−3a=4 ((−3a)/(2(√(−3a+b))))=−(1/4) 6a=(√(−3a+b)) 36a^2 =−3a+b=4 a^2 =(1/9) a=±(1/3) b=4±1 (((√((x/3)+5))−2)/(x+3)) (((√(−(x/3)+3))−2)/(x+3))

$$\sqrt{−\mathrm{3}{a}+{b}}−\mathrm{2}=\mathrm{0} \\ $$$${b}−\mathrm{3}{a}=\mathrm{4} \\ $$$$\frac{−\mathrm{3}{a}}{\mathrm{2}\sqrt{−\mathrm{3}{a}+{b}}}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{6}{a}=\sqrt{−\mathrm{3}{a}+{b}} \\ $$$$\mathrm{36}{a}^{\mathrm{2}} =−\mathrm{3}{a}+{b}=\mathrm{4} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${a}=\pm\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${b}=\mathrm{4}\pm\mathrm{1} \\ $$$$\frac{\sqrt{\frac{{x}}{\mathrm{3}}+\mathrm{5}}−\mathrm{2}}{{x}+\mathrm{3}} \\ $$$$\frac{\sqrt{−\frac{{x}}{\mathrm{3}}+\mathrm{3}}−\mathrm{2}}{{x}+\mathrm{3}} \\ $$

Answered by iloveisrael last updated on 26/May/21

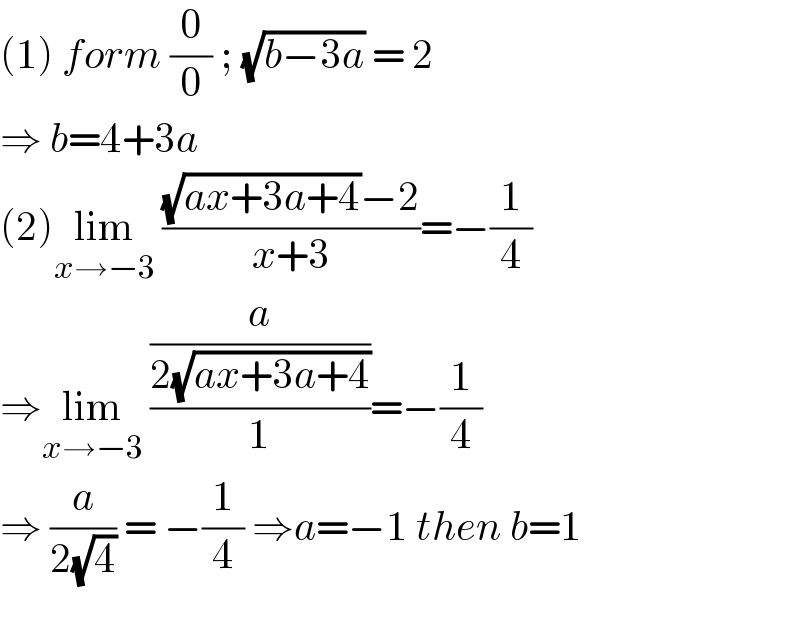
(1) form (0/0) ; (√(b−3a)) = 2 ⇒ b=4+3a (2)lim_(x→−3) (((√(ax+3a+4))−2)/(x+3))=−(1/4) ⇒lim_(x→−3) ((a/(2(√(ax+3a+4))))/1)=−(1/4) ⇒ (a/(2(√4))) = −(1/4) ⇒a=−1 then b=1

$$\left(\mathrm{1}\right)\:{form}\:\frac{\mathrm{0}}{\mathrm{0}}\:;\:\sqrt{{b}−\mathrm{3}{a}}\:=\:\mathrm{2}\: \\ $$$$\Rightarrow\:{b}=\mathrm{4}+\mathrm{3}{a} \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{\sqrt{{ax}+\mathrm{3}{a}+\mathrm{4}}−\mathrm{2}}{{x}+\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{\frac{{a}}{\mathrm{2}\sqrt{{ax}+\mathrm{3}{a}+\mathrm{4}}}}{\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\frac{{a}}{\mathrm{2}\sqrt{\mathrm{4}}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{a}=−\mathrm{1}\:{then}\:{b}=\mathrm{1} \\ $$$$ \\ $$

Answered by Willson last updated on 26/May/21

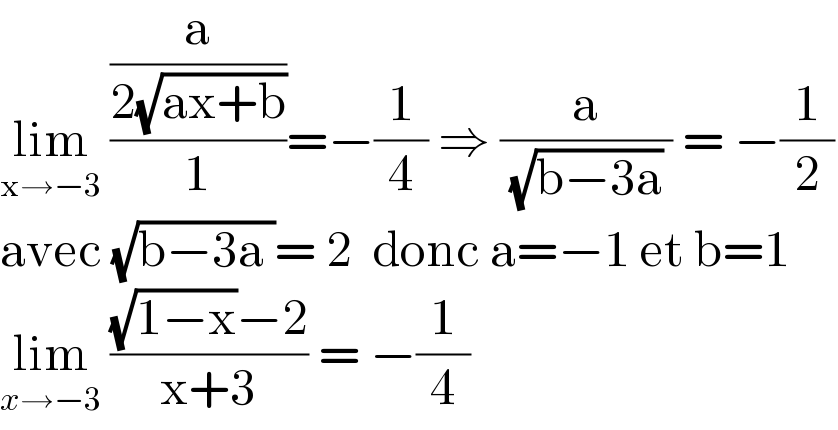
lim_(x→−3) ((a/(2(√(ax+b))))/1)=−(1/4) ⇒ (a/( (√(b−3a)) )) = −(1/2) avec (√(b−3a ))= 2 donc a=−1 et b=1 lim_(x→−3) (((√(1−x))−2)/(x+3)) = −(1/4)

$$\underset{\mathrm{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{\frac{\mathrm{a}}{\mathrm{2}\sqrt{\mathrm{ax}+\mathrm{b}}}}{\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:\frac{\mathrm{a}}{\:\sqrt{\mathrm{b}−\mathrm{3a}}\:}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{avec}\:\sqrt{\mathrm{b}−\mathrm{3a}\:}=\:\mathrm{2}\:\:\mathrm{donc}\:\mathrm{a}=−\mathrm{1}\:\mathrm{et}\:\mathrm{b}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\mathrm{x}}−\mathrm{2}}{\mathrm{x}+\mathrm{3}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply