Question Number 142079 by rs4089 last updated on 26/May/21
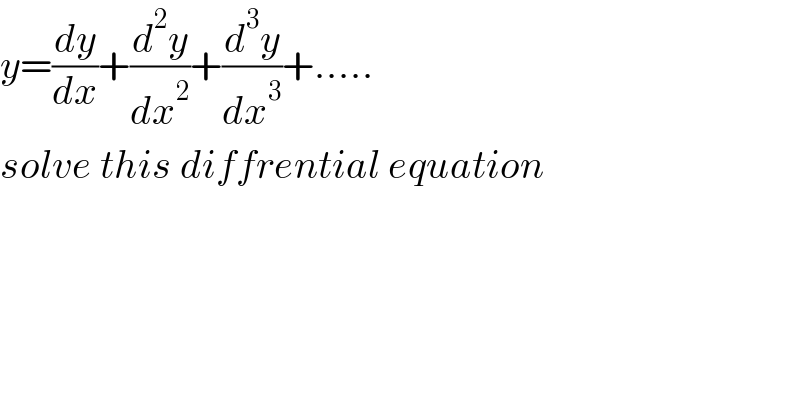
$${y}=\frac{{dy}}{{dx}}+\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }+….. \\ $$$${solve}\:{this}\:{diffrential}\:{equation} \\ $$
Answered by Dwaipayan Shikari last updated on 26/May/21
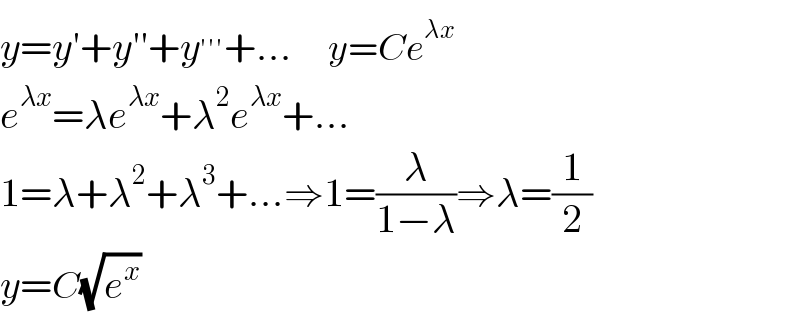
$${y}={y}'+{y}''+{y}^{'''} +…\:\:\:\:\:\:{y}={Ce}^{\lambda{x}} \\ $$$${e}^{\lambda{x}} =\lambda{e}^{\lambda{x}} +\lambda^{\mathrm{2}} {e}^{\lambda{x}} +… \\ $$$$\mathrm{1}=\lambda+\lambda^{\mathrm{2}} +\lambda^{\mathrm{3}} +…\Rightarrow\mathrm{1}=\frac{\lambda}{\mathrm{1}−\lambda}\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}={C}\sqrt{{e}^{{x}} } \\ $$
Answered by mindispower last updated on 26/May/21
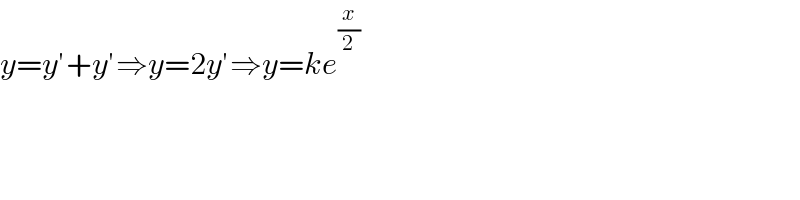
$${y}={y}'+{y}'\Rightarrow{y}=\mathrm{2}{y}'\Rightarrow{y}={ke}^{\frac{{x}}{\mathrm{2}}} \\ $$
Answered by mnjuly1970 last updated on 26/May/21
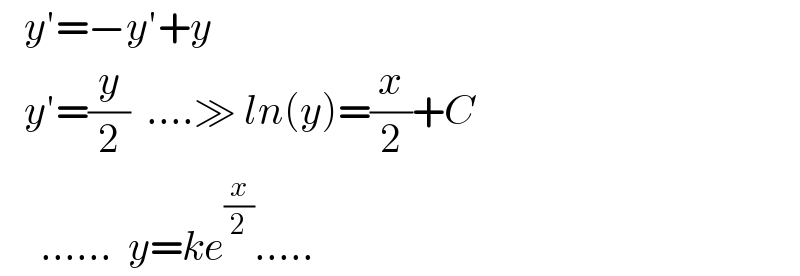
$$\:\:\:{y}'=−{y}'+{y} \\ $$$$\:\:\:{y}'=\frac{{y}}{\mathrm{2}}\:\:….\gg\:{ln}\left({y}\right)=\frac{{x}}{\mathrm{2}}+{C} \\ $$$$\:\:\:\:\:……\:\:{y}={ke}^{\frac{{x}}{\mathrm{2}}} ….. \\ $$
