Question Number 11036 by suci last updated on 08/Mar/17
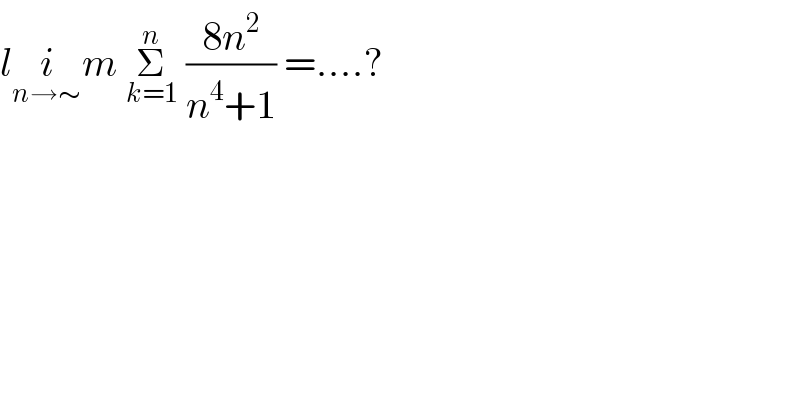
$${l}\underset{{n}\rightarrow\sim} {{i}m}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{8}{n}^{\mathrm{2}} }{{n}^{\mathrm{4}} +\mathrm{1}}\:=….? \\ $$
Commented by FilupS last updated on 08/Mar/17
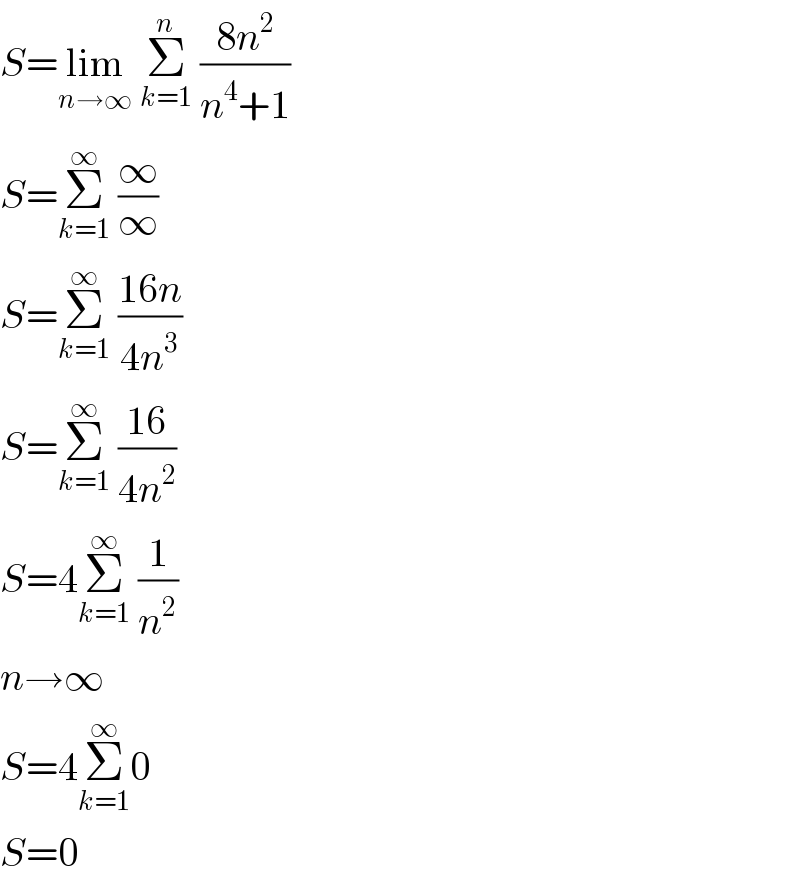
$${S}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{8}{n}^{\mathrm{2}} }{{n}^{\mathrm{4}} +\mathrm{1}} \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\infty}{\infty} \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{16}{n}}{\mathrm{4}{n}^{\mathrm{3}} } \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{16}}{\mathrm{4}{n}^{\mathrm{2}} } \\ $$$${S}=\mathrm{4}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$${n}\rightarrow\infty \\ $$$${S}=\mathrm{4}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{0} \\ $$$${S}=\mathrm{0} \\ $$
Answered by ajfour last updated on 09/Mar/17

$$\mathrm{2}\pi\sqrt{\mathrm{2}}\:\:. \\ $$
Commented by ajfour last updated on 09/Mar/17
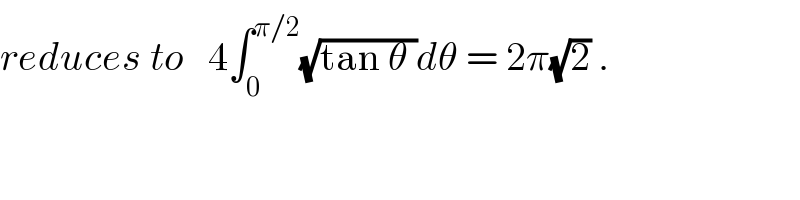
$${reduces}\:{to}\:\:\:\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \sqrt{\mathrm{tan}\:\theta\:}{d}\theta\:=\:\mathrm{2}\pi\sqrt{\mathrm{2}}\:. \\ $$
Commented by FilupS last updated on 09/Mar/17

$$\mathrm{proof}? \\ $$
Commented by ajfour last updated on 12/Mar/17
![L=lim_(n→∞ ) Σ_(k=1) ^n (((8k^2 )/(k^4 +1))) L=lim_(n→∞ ) S_n S_n =(8/n) Σ_(k=1) ^n (((k/n)^2 )/((k/n)^4 +(1/n)^4 )) ((1/n)) now (k/n) =x ; (1/n)=(((k+1)−k)/n) =dx S_n = (8/n)∫_0 ^1 (x^2 /(x^4 +a^4 )) dx where (1/n^4 ) =a^4 (for ease) let x^2 =a^2 tan θ⇒x=a(√(tan θ)) ⇒ x^4 +a^4 =a^4 sec^2 θ dx=((asec^2 θdθ)/(2(√(tan θ)))) , substituting S_n =(8/n)∫_0 ^(π/2) (((a^3 /2)sec^2 θ(√(tan θ))dθ)/(a^4 sec^2 θ)) L=lim_(n→∞ ) [ (8/(2na))∫_0 ^(π/2) (√(tan θ)) dθ] as n→ ∞, na→1 for a^4 =(1/n^4 ) so L= 4∫_0 ^(π/2) (√(tan θ)) dθ L=4((π/( (√2))))=2π(√2) .](https://www.tinkutara.com/question/Q11107.png)
$${L}={lim}_{{n}\rightarrow\infty\:} \underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{8}{k}^{\mathrm{2}} }{{k}^{\mathrm{4}} +\mathrm{1}}\right) \\ $$$${L}={lim}_{{n}\rightarrow\infty\:} {S}_{{n}} \\ $$$${S}_{{n}} =\frac{\mathrm{8}}{{n}}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\left({k}/{n}\right)^{\mathrm{2}} }{\left({k}/{n}\right)^{\mathrm{4}} +\left(\mathrm{1}/{n}\right)^{\mathrm{4}} }\:\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$${now}\:\frac{{k}}{{n}}\:={x}\:;\:\frac{\mathrm{1}}{{n}}=\frac{\left({k}+\mathrm{1}\right)−{k}}{{n}}\:={dx} \\ $$$${S}_{{n}} =\:\frac{\mathrm{8}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +{a}^{\mathrm{4}} }\:{dx}\: \\ $$$${where}\:\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\:={a}^{\mathrm{4}} \:\left({for}\:{ease}\right) \\ $$$${let}\:{x}^{\mathrm{2}} ={a}^{\mathrm{2}} \mathrm{tan}\:\theta\Rightarrow{x}={a}\sqrt{\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\:{x}^{\mathrm{4}} +{a}^{\mathrm{4}} ={a}^{\mathrm{4}} \mathrm{sec}\:^{\mathrm{2}} \theta \\ $$$${dx}=\frac{{a}\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{\mathrm{2}\sqrt{\mathrm{tan}\:\theta}}\:\:,\:{substituting} \\ $$$${S}_{{n}} =\frac{\mathrm{8}}{{n}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\:\frac{\left({a}^{\mathrm{3}} /\mathrm{2}\right)\mathrm{sec}\:^{\mathrm{2}} \theta\sqrt{\mathrm{tan}\:\theta}{d}\theta}{{a}^{\mathrm{4}} \mathrm{sec}\:^{\mathrm{2}} \theta} \\ $$$$\:\:{L}={lim}_{{n}\rightarrow\infty\:\:} \left[\:\frac{\mathrm{8}}{\mathrm{2}{na}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\sqrt{\mathrm{tan}\:\theta}\:{d}\theta\right] \\ $$$$\:\:{as}\:{n}\rightarrow\:\infty,\:{na}\rightarrow\mathrm{1}\:{for}\:{a}^{\mathrm{4}} =\frac{\mathrm{1}}{{n}^{\mathrm{4}} } \\ $$$${so}\:{L}=\:\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\sqrt{\mathrm{tan}\:\theta}\:{d}\theta \\ $$$${L}=\mathrm{4}\left(\frac{\pi}{\:\sqrt{\mathrm{2}}}\right)=\mathrm{2}\pi\sqrt{\mathrm{2}}\:\:. \\ $$
Commented by FilupS last updated on 12/Mar/17

$$\mathrm{oh},\:\mathrm{they}\:\mathrm{made}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}. \\ $$$$\mathrm{i}\:\mathrm{see}\:\mathrm{now} \\ $$
Commented by ajfour last updated on 12/Mar/17

$${the}\:\Sigma\:{should}\:{make}\:{sense}. \\ $$
Answered by DrDaveR last updated on 22/Mar/17
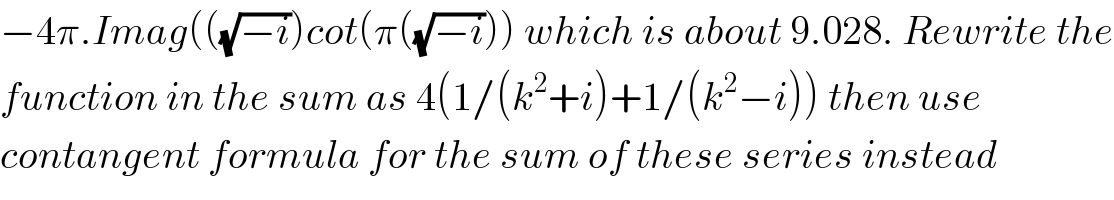
$$−\mathrm{4}\pi.{Imag}\left(\left(\sqrt{−{i}}\right){cot}\left(\pi\left(\sqrt{−{i}}\right)\right)\:{which}\:{is}\:{about}\:\mathrm{9}.\mathrm{028}.\:{Rewrite}\:{the}\right. \\ $$$${function}\:{in}\:{the}\:{sum}\:{as}\:\mathrm{4}\left(\mathrm{1}/\left({k}^{\mathrm{2}} +{i}\right)+\mathrm{1}/\left({k}^{\mathrm{2}} −{i}\right)\right)\:{then}\:{use}\: \\ $$$${contangent}\:{formula}\:{for}\:{the}\:{sum}\:{of}\:{these}\:{series}\:{instead} \\ $$
