Question Number 11042 by Mahmoud A.R last updated on 09/Mar/17
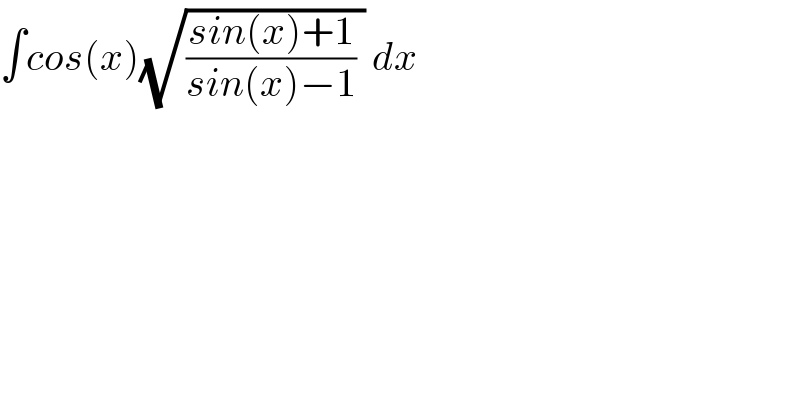
$$\int{cos}\left({x}\right)\sqrt{\frac{{sin}\left({x}\right)+\mathrm{1}}{{sin}\left({x}\right)−\mathrm{1}}\:}\:{dx} \\ $$
Answered by ajfour last updated on 09/Mar/17
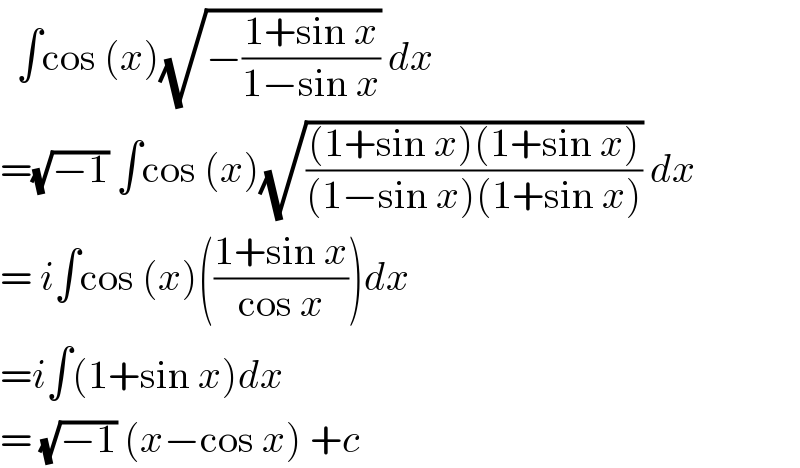
$$\:\:\int\mathrm{cos}\:\left({x}\right)\sqrt{−\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}}\:{dx} \\ $$$$=\sqrt{−\mathrm{1}}\:\int\mathrm{cos}\:\left({x}\right)\sqrt{\frac{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\left(\mathrm{1}+\mathrm{sin}\:{x}\right)}{\left(\mathrm{1}−\mathrm{sin}\:{x}\right)\left(\mathrm{1}+\mathrm{sin}\:{x}\right)}}\:{dx} \\ $$$$=\:{i}\int\mathrm{cos}\:\left({x}\right)\left(\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\right){dx} \\ $$$$={i}\int\left(\mathrm{1}+\mathrm{sin}\:{x}\right){dx} \\ $$$$=\:\sqrt{−\mathrm{1}}\:\left({x}−\mathrm{cos}\:{x}\right)\:+{c} \\ $$
Commented by Mahmoud A.R last updated on 09/Mar/17

$${thanks}\:{alot} \\ $$
