Question Number 11095 by FilupS last updated on 12/Mar/17

$$\mathrm{You}\:\mathrm{have}\:\mathrm{a}\:\mathrm{line}\:\mathrm{of}\:\mathrm{length}\:\mathrm{1}. \\ $$$$\mathrm{You}\:\mathrm{place}\:\mathrm{two}\:\mathrm{random}\:\mathrm{points}\:\mathrm{on}\:\mathrm{the}\:\mathrm{line}. \\ $$$$\: \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{average}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{the}\:\mathrm{two}\:\mathrm{points}?\:\mathrm{Please}\:\mathrm{show}\:\mathrm{your}\:\mathrm{working}. \\ $$
Commented by FilupS last updated on 12/Mar/17
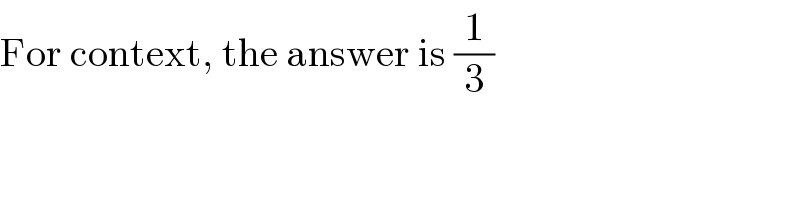
$$\mathrm{For}\:\mathrm{context},\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by ajfour last updated on 12/Mar/17

$$\frac{\mathrm{1}}{\mathrm{4}}.\: \\ $$
Commented by FilupS last updated on 12/Mar/17

$$\mathrm{incorrect} \\ $$$$\: \\ $$$$\mathrm{please}\:\mathrm{show}\:\mathrm{working}. \\ $$$$\: \\ $$$$\mathrm{it}\:\mathrm{helps}\:\mathrm{to}\:\mathrm{see}\:\mathrm{mistakes},\:\mathrm{etc}. \\ $$
Commented by ajfour last updated on 12/Mar/17
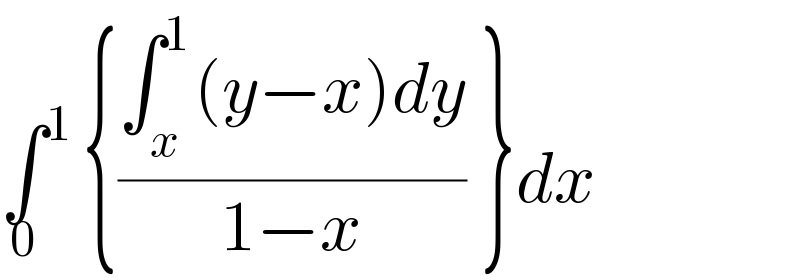
$$\underset{\mathrm{0}} {\int}^{\mathrm{1}\:} \left\{\frac{\int_{{x}} ^{\mathrm{1}} \left({y}−{x}\right){dy}}{\mathrm{1}−{x}}\:\right\}{dx} \\ $$
Commented by FilupS last updated on 12/Mar/17

$$\mathrm{Please}\:\mathrm{explain}\:\mathrm{where}\:\mathrm{you}\:\mathrm{derived} \\ $$$$\mathrm{this}\:\mathrm{result}? \\ $$
Answered by ajfour last updated on 12/Mar/17
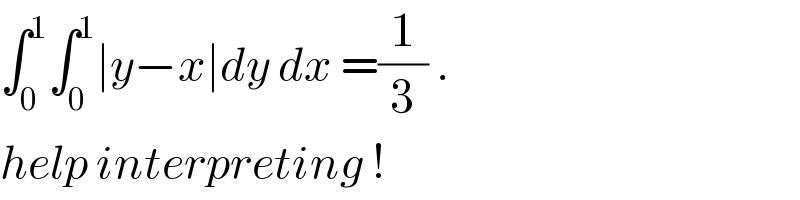
$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \mid{y}−{x}\mid{dy}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\:. \\ $$$${help}\:{interpreting}\:! \\ $$
Commented by FilupS last updated on 12/Mar/17

$$\mathrm{Although}\:\mathrm{this}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{solution}, \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{unsure}\:\mathrm{that}\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{correct}\:\mathrm{method} \\ $$$$\mathrm{of}\:\mathrm{approaching}\:\mathrm{the}\:\mathrm{problem}. \\ $$$$\: \\ $$$$\mathrm{The}\:\mathrm{method}\:\mathrm{I}\:\mathrm{am}\:\mathrm{aware}\:\mathrm{of}\:\mathrm{is}\:\mathrm{via} \\ $$$$\mathrm{probability}\:\mathrm{density} \\ $$
Commented by FilupS last updated on 12/Mar/17
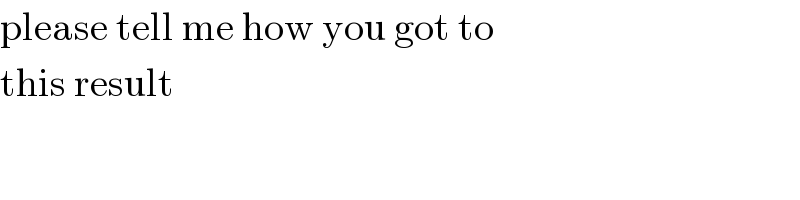
$$\mathrm{please}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{how}\:\mathrm{you}\:\mathrm{got}\:\mathrm{to} \\ $$$$\mathrm{this}\:\mathrm{result} \\ $$
Commented by ajfour last updated on 12/Mar/17

Commented by FilupS last updated on 12/Mar/17

$$\mathrm{Although}\:\mathrm{you}\:\mathrm{have}\:\mathrm{gotten}\:\mathrm{the}\:\mathrm{same}\:\mathrm{result}, \\ $$$$\mathrm{i}\:\mathrm{think}\:\mathrm{you}\:\mathrm{have}\:\mathrm{solved}\:\mathrm{for}\:\mathrm{a}\:\mathrm{similar} \\ $$$$\mathrm{question}\:\mathrm{where}\:\left({x},\:{y}\right)\rightarrow\mathbb{R}^{\mathrm{2}} \\ $$$$\: \\ $$$$\mathrm{I}\:\mathrm{beleive}\:\mathrm{this}\:\mathrm{question}\:\mathrm{has}\:\left({x},\:{y}\right)\rightarrow\mathbb{R}^{\mathrm{1}} \\ $$$$\: \\ $$$$\mathrm{I}\:\mathrm{honestly}\:\mathrm{don}'\mathrm{t}\:\mathrm{know} \\ $$$$\: \\ $$$$\mathrm{The}\:\mathrm{method}\:\mathrm{I}\:\mathrm{am}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{has}\:\mathrm{to}\:\mathrm{do} \\ $$$$\mathrm{with}\:\mathrm{probability} \\ $$
Commented by ajfour last updated on 12/Mar/17
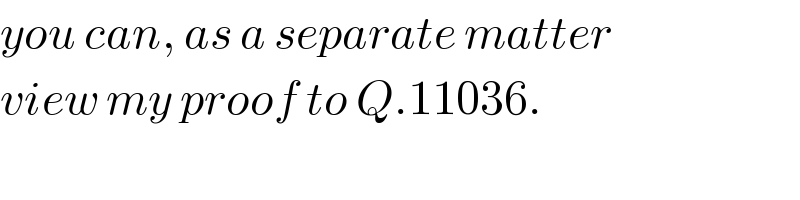
$${you}\:{can},\:{as}\:{a}\:{separate}\:{matter} \\ $$$${view}\:{my}\:{proof}\:{to}\:{Q}.\mathrm{11036}. \\ $$
