Question Number 11148 by suci last updated on 14/Mar/17
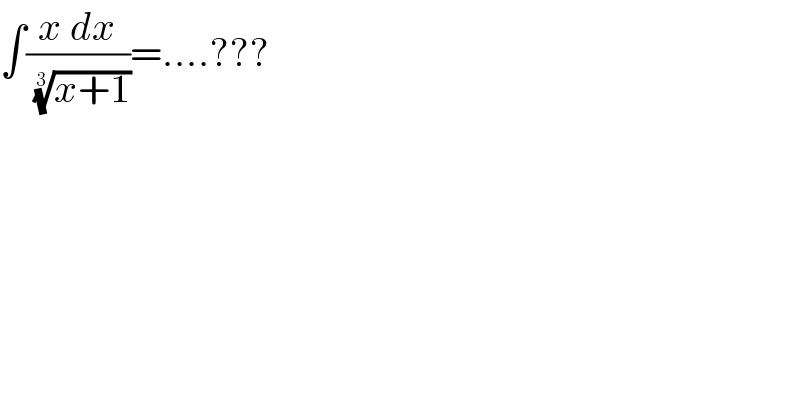
$$\int\frac{{x}\:{dx}}{\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}}=….??? \\ $$
Answered by ajfour last updated on 14/Mar/17
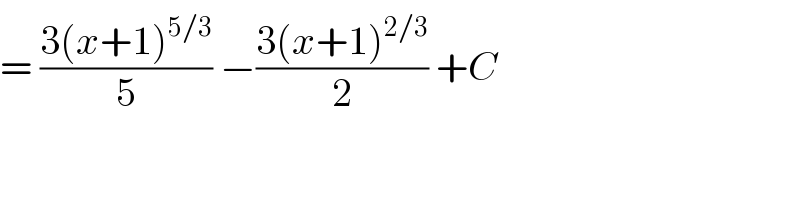
$$=\:\frac{\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{5}/\mathrm{3}} }{\mathrm{5}}\:−\frac{\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} }{\mathrm{2}}\:+{C}\: \\ $$
Commented by ajfour last updated on 14/Mar/17
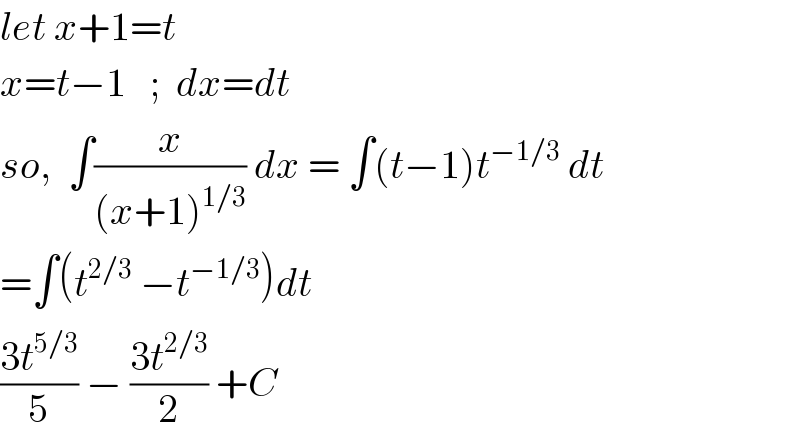
$${let}\:{x}+\mathrm{1}={t} \\ $$$${x}={t}−\mathrm{1}\:\:\:;\:\:{dx}={dt} \\ $$$${so},\:\:\int\frac{{x}}{\left({x}+\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} }\:{dx}\:=\:\int\left({t}−\mathrm{1}\right){t}^{−\mathrm{1}/\mathrm{3}} \:{dt} \\ $$$$=\int\left({t}^{\mathrm{2}/\mathrm{3}} \:−{t}^{−\mathrm{1}/\mathrm{3}} \right){dt} \\ $$$$\frac{\mathrm{3}{t}^{\mathrm{5}/\mathrm{3}} }{\mathrm{5}}\:−\:\frac{\mathrm{3}{t}^{\mathrm{2}/\mathrm{3}} }{\mathrm{2}}\:+{C}\:\: \\ $$
Commented by chux last updated on 17/Mar/17

$$\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{1}…..\left(\mathrm{1}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{35}…..\left(\mathrm{2}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +\mathrm{z}^{\mathrm{3}} =\mathrm{97}…..\left(\mathrm{3}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\mathrm{solve}\:\mathrm{the}\:\mathrm{equation} \\ $$
Commented by ajfour last updated on 17/Mar/17
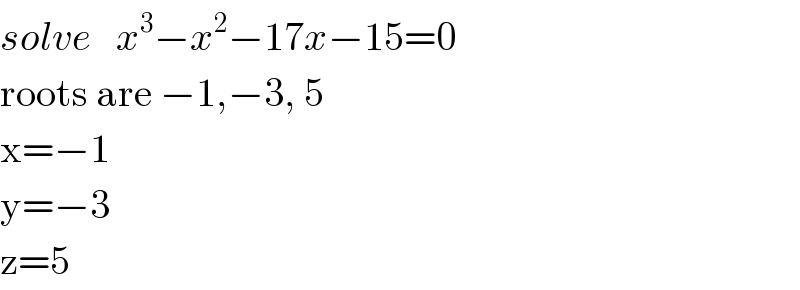
$${solve}\:\:\:{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{17}{x}−\mathrm{15}=\mathrm{0} \\ $$$$\mathrm{roots}\:\mathrm{are}\:−\mathrm{1},−\mathrm{3},\:\mathrm{5} \\ $$$$\mathrm{x}=−\mathrm{1} \\ $$$$\mathrm{y}=−\mathrm{3} \\ $$$$\mathrm{z}=\mathrm{5} \\ $$
