Menu Close

nice-calculus-prove-that-1-0-1-li-2-1-x-2-pi-2-2-4-2-0-1-log-1-t-t-3-4-1-t-dt-pi-3-2-2-2-3-4-log-2-pi-2-hi

Tinku Tara 0 Comments
Pin




Question Number 131991 by mnjuly1970 last updated on 10/Feb/21
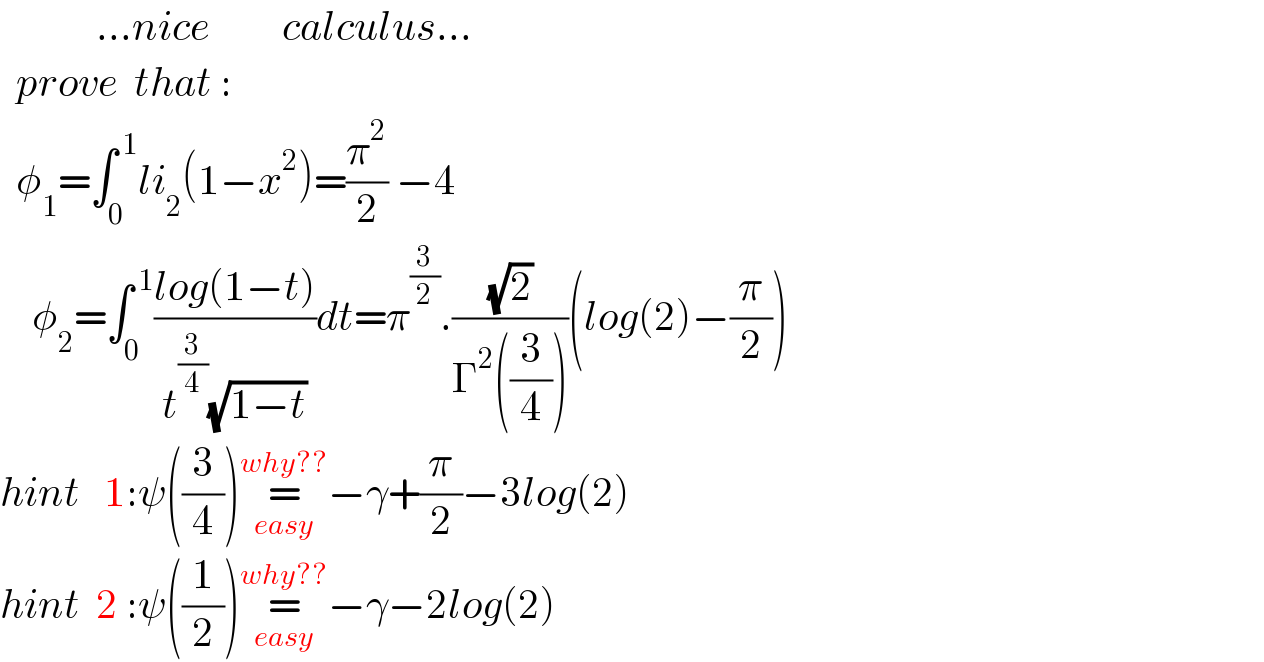
...nice calculus... prove that : φ_1 =∫_0 ^( 1) li_2 (1−x^2 )=(π^2 /2) −4 φ_2 =∫_0 ^( 1) ((log(1−t))/(t^(3/4) (√(1−t))))dt=π^(3/2) .((√2)/(Γ^2 ((3/4))))(log(2)−(π/2)) hint 1:ψ((3/4))=_(easy) ^(why??) −γ+(π/2)−3log(2) hint 2 :ψ((1/2))=_(easy) ^(why??) −γ−2log(2)
$$\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:\:\:\:\:\:\:\:{calculus}…\:\: \\ $$$$\:\:{prove}\:\:{that}\:: \\ $$$$\:\:\phi_{\mathrm{1}} =\int_{\mathrm{0}} ^{\:\mathrm{1}} {li}_{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:−\mathrm{4} \\ $$$$\:\:\:\:\phi_{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{log}\left(\mathrm{1}−{t}\right)}{{t}^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{1}−{t}}}{dt}=\pi^{\frac{\mathrm{3}}{\mathrm{2}}} .\frac{\sqrt{\mathrm{2}}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}\left({log}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{2}}\right) \\ $$$${hint}\:\:\:\mathrm{1}:\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\underset{{easy}} {\overset{{why}??} {=}}−\gamma+\frac{\pi}{\mathrm{2}}−\mathrm{3}{log}\left(\mathrm{2}\right) \\ $$$${hint}\:\:\mathrm{2}\::\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\underset{{easy}} {\overset{{why}??} {=}}−\gamma−\mathrm{2}{log}\left(\mathrm{2}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 10/Feb/21
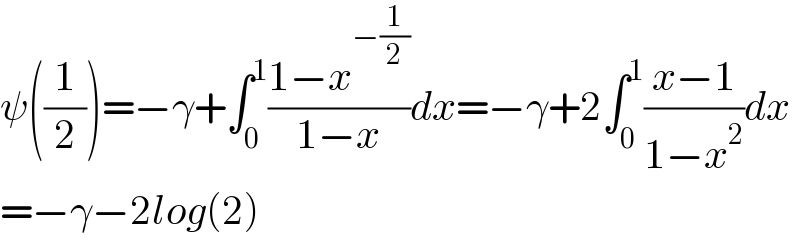
ψ((1/2))=−γ+∫_0 ^1 ((1−x^(−(1/2)) )/(1−x))dx=−γ+2∫_0 ^1 ((x−1)/(1−x^2 ))dx =−γ−2log(2)
$$\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{x}}{dx}=−\gamma+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$=−\gamma−\mathrm{2}{log}\left(\mathrm{2}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 10/Feb/21
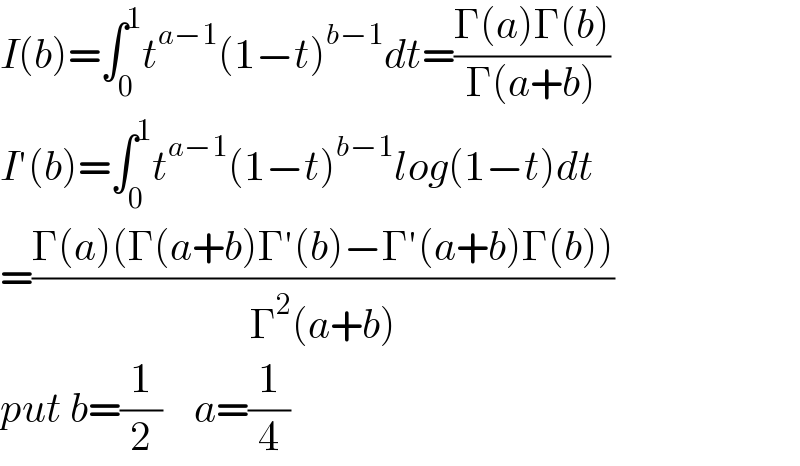
I(b)=∫_0 ^1 t^(a−1) (1−t)^(b−1) dt=((Γ(a)Γ(b))/(Γ(a+b))) I′(b)=∫_0 ^1 t^(a−1) (1−t)^(b−1) log(1−t)dt =((Γ(a)(Γ(a+b)Γ′(b)−Γ′(a+b)Γ(b)))/(Γ^2 (a+b))) put b=(1/2) a=(1/4)
$${I}\left({b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{b}−\mathrm{1}} {dt}=\frac{\Gamma\left({a}\right)\Gamma\left({b}\right)}{\Gamma\left({a}+{b}\right)} \\ $$$${I}'\left({b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{b}−\mathrm{1}} {log}\left(\mathrm{1}−{t}\right){dt} \\ $$$$=\frac{\Gamma\left({a}\right)\left(\Gamma\left({a}+{b}\right)\Gamma'\left({b}\right)−\Gamma'\left({a}+{b}\right)\Gamma\left({b}\right)\right)}{\Gamma^{\mathrm{2}} \left({a}+{b}\right)} \\ $$$${put}\:{b}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:{a}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *