Question Number 11167 by agni5 last updated on 15/Mar/17
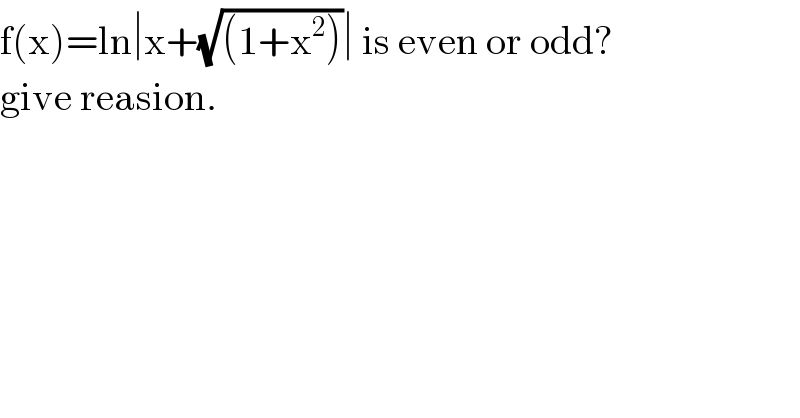
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ln}\mid\mathrm{x}+\sqrt{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mid\:\mathrm{is}\:\mathrm{even}\:\mathrm{or}\:\mathrm{odd}?\: \\ $$$$\mathrm{give}\:\mathrm{reasion}. \\ $$
Answered by mrW1 last updated on 15/Mar/17
![f(x)=ln∣x+(√((1+x^2 )))∣=ln (x+(√(1+x^2 ))) f(−x)=ln[−x+(√(1+(−x)^2 ))] =ln(−x+(√(1+x^2 ))) =ln[(−x+(√(1+x^2 )))×((x+(√(1+x^2 )))/(x+(√(1+x^2 ))))] =ln ((1+x^2 −x^2 )/(x+(√(1+x^2 )))) =ln (1/(x+(√(1+x^2 )))) =−ln (x+(√(1+x^2 ))) =−f(x) ⇒f(x) is odd.](https://www.tinkutara.com/question/Q11168.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ln}\mid\mathrm{x}+\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\mid=\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right) \\ $$$$\mathrm{f}\left(−\mathrm{x}\right)=\mathrm{ln}\left[−\mathrm{x}+\sqrt{\mathrm{1}+\left(−{x}\right)^{\mathrm{2}} }\right] \\ $$$$=\mathrm{ln}\left(−\mathrm{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{ln}\left[\left(−\mathrm{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)×\frac{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right] \\ $$$$=\mathrm{ln}\:\frac{\mathrm{1}+{x}^{\mathrm{2}} −{x}^{\mathrm{2}} }{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$=\mathrm{ln}\:\frac{\mathrm{1}}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$=−\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right) \\ $$$$=−{f}\left({x}\right) \\ $$$$ \\ $$$$\Rightarrow{f}\left({x}\right)\:{is}\:{odd}. \\ $$
Answered by ajfour last updated on 15/Mar/17
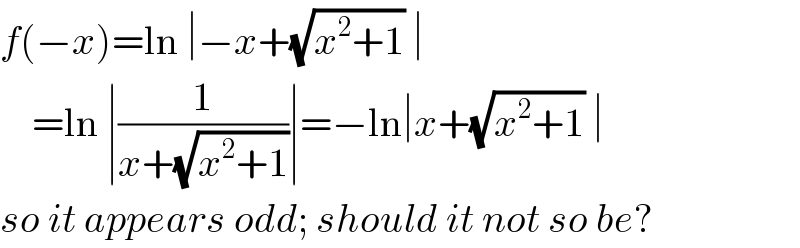
$${f}\left(−{x}\right)=\mathrm{ln}\:\mid−{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\mid \\ $$$$\:\:\:\:=\mathrm{ln}\:\mid\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\mid=−\mathrm{ln}\mid{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\mid \\ $$$${so}\:{it}\:{appears}\:{odd};\:{should}\:{it}\:{not}\:{so}\:{be}? \\ $$
