Question Number 76714 by peter frank last updated on 29/Dec/19
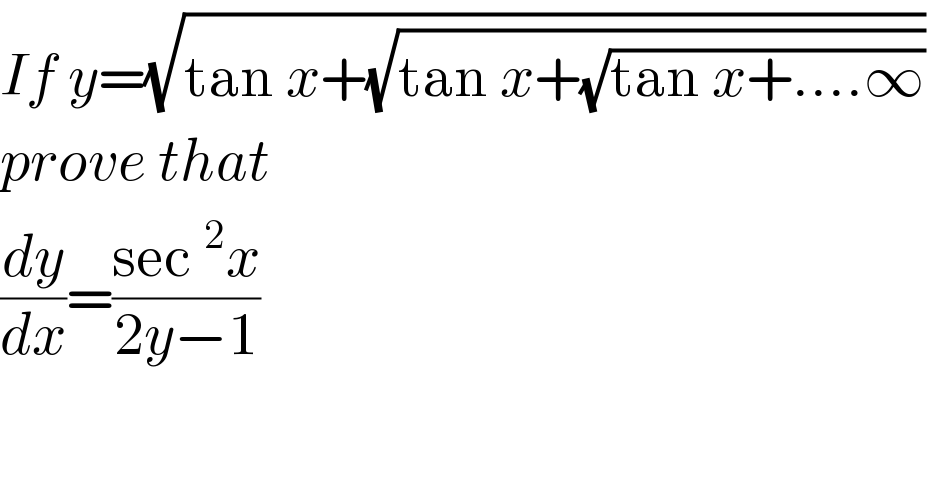
$${If}\:{y}=\sqrt{\mathrm{tan}\:{x}+\sqrt{\mathrm{tan}\:{x}+\sqrt{\mathrm{tan}\:{x}+….\infty}}}\: \\ $$$${prove}\:{that} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{sec}\:^{\mathrm{2}} {x}}{\mathrm{2}{y}−\mathrm{1}} \\ $$
Answered by mind is power last updated on 29/Dec/19
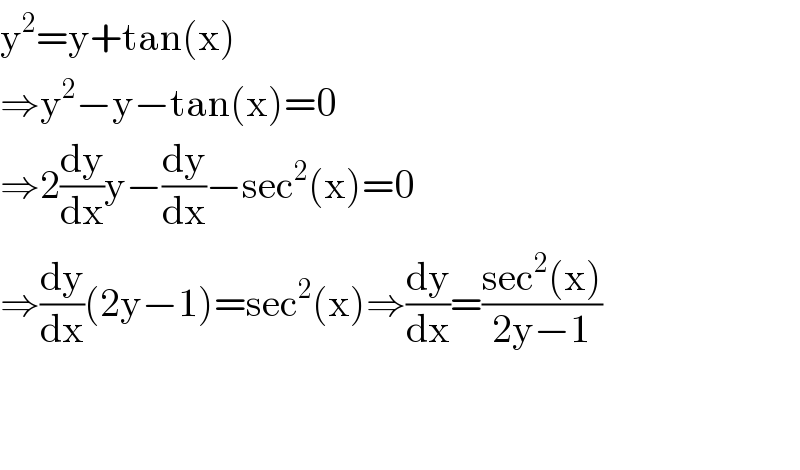
$$\mathrm{y}^{\mathrm{2}} =\mathrm{y}+\mathrm{tan}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{y}^{\mathrm{2}} −\mathrm{y}−\mathrm{tan}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\frac{\mathrm{dy}}{\mathrm{dx}}\mathrm{y}−\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{sec}^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}\left(\mathrm{2y}−\mathrm{1}\right)=\mathrm{sec}^{\mathrm{2}} \left(\mathrm{x}\right)\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{sec}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{2y}−\mathrm{1}} \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 30/Dec/19

$${thank}\:{you} \\ $$
